Nombres complexes, bac Sti2d

Nombres complexes, bac Sti2d.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

On considère le nombre complexe z = 2e^{−i p/4} où i est le nombre complexe de module 1 et d’argument ½p.
Le carré de z est égal à : a) −4i ; b) −4 ; c) −2i ; d) 4.
z² = 4 e^{−i
p/2} =4(cos (-p/2)+i sin(-p/2) = -4i.
L’inverse de z est égal à : a) ½e^{−i
p/4} ; b) -2e^{−i
p/4} ; c) 2e^{i
p/4} ; d) ½ e^{i
p/4}.
1/z = 1/(2e^{−i
p/4}) =½e^{i
p/4}.

Le plan complexe est rapporté à un repère orthonormal direct. On note C l’ensemble des nombres complexes, et i le nombre complexe de module 1 et d’argument p/2..
1. On considère l’équation (E) d’inconnue z :
(2−i)z = 2−6i.
Résoudre dans C l’équation (E). On notera z₁ la solution de (E) que l’on écrira sous forme algébrique.
z₁ =(2-6i) /(2-i) =(2-6i)(2+i) / ((2+i)(2-i)) =(4-6i²-10i) /(4-i²)=10(1-i)/5=2(1-i).
Déterminer la forme exponentielle de z₁.
Module de z₁ : 2(1+1)^½ =2*2^½~2,828 ; argument : arctan(-1) =-p/4 ; z₁ = 2*2^½e^-ip/4.
Soit z₂ le nombre complexe défini par : z₂ = e^{−i p/2}x z₁.
Déterminer les formes exponentielle et algébrique de z₂.
z₂ = e^{−i p/2}x 2*2^½e^-ip/4 =2*2^½e^-i3p/4.
z₂ ==2*2^½(cos(-3p/4) +i sin(-3p/4)) =2*2^½(-0,707-0,707 i) =2(-1-i).
Soit A, B et C les points du plan d’affixes respectives : z_A = 2−2i, z_B = −2−2i et z_C = −4i.
Placer les points A, B et C dans le plan complexe.
Déterminer la nature du triangle ABC.

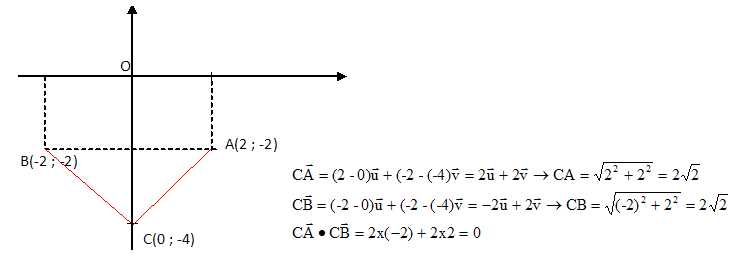
Le triangle ABC est rectangle isocèle.

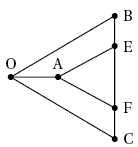
On considère le puzzle représenté ci-deoous. Il est constitué de 3 pièces : le triangle AEF et les quadrilatères AEBO et AFCO, découpés dans le triangle OBC. Le plan complexe est rapporté à un repère orthonormal direct
d’unité graphique 1 cm.

Résoudre dans l’ensemble des nombres complexes l’équation d’inconnue complexe z :

.
.

.

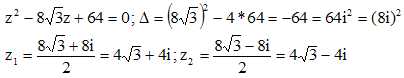
On considère les points B et C d'affixes respectives _zB = 4*3^½+4i et z_C =4*3^½-4i. Vérifier que z_B = 8 e^(ip/6).
Module de z_B :((4*3^½)²+4²)^½ =64^½ =8 ; argument de z_B : arctan(4/(4*3^½)) =p/6.
En déduire une écriture exponentielle de z_C.
z_B et z_C sont conjugués : z_C = 8 e^(-ip/6).
Placer les points B et C dans le repère défini précédemment. Voir ci-dessous.
Démontrer que le triangle OBC est équilatéral.
OB =|z_B|=8 ; OC =|z_C|=8 ; x_C-x_B =4*3^½-4*3^½+ =0 ; y_C-y_B =-4-4 = -8 ; BC = (0²+(-8)²)^½ = 8.
Les trois côtés du triangle sont égaux : le triangle OBC est équilatéral.
Le point A a pour coordonnées (3 ; 0). Le point D a pour coordonnées 4*3^½ ; 0) .
Écrire les affixes des points z_A et z_D des points A et D.
z_A =3 +0i =3 ; z_D =4*3^½ +0i =4*3^½ .
Calculer les affixes du point E milieu du segment [BD] et du point F milieu du segment [CD].
x_E =½(x_B+x_D) =½(4*3^½+4*3^½ )=4*3^½ ; y_E =½(y_B+y_D) =½(4+0 )=2 ; z_E = 4*3^½ +2i.
x_F =½(x_C+x_D) =½(4*3^½+4*3^½ )=4*3^½ ; y_F =½(y_C+y_D) =½(-4+0 )=-2 ; z_F = 4*3^½ -2i.
Placer les points A, D, E et F dans le repère.

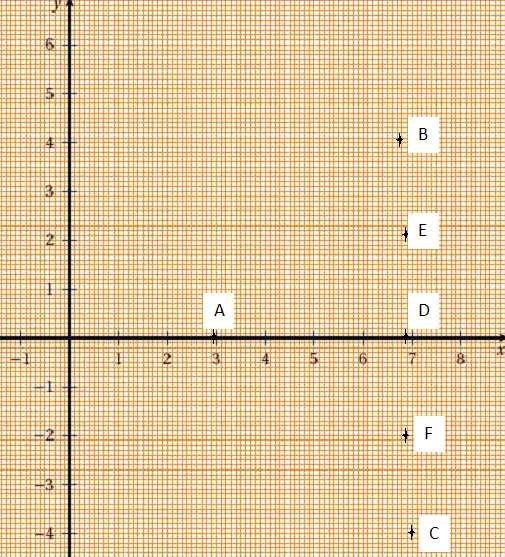
Calculer l’aire exacte, en cm², du triangle AEF.
AD *EF / 2 avec AD =((x_D-x_A)² +(y_D-y_A)² )^½ =((4*3^½-3)² +(0-0)² )^½ = 4*3^½-3.
EF =((x_F-x_E)² +(y_F-y_E)² )^½ =((4*3^½-4*3^½)² +(-2-2)² )^½ = 4.
AD *EF / 2 =2( 4*3^½-3) ~7,86 cm².
Quelles sont les valeurs exactes, en cm², des aires des deux autres pièces du puzzle ?
Aire du triangle OBC : ½BC * OD avec BC =((x_C-x_B)² +(y_C-y_B)² )^½ =((4*3^½-4*3^½)² +(-4-4)² )^½ = 8.
OD =((x_D-x_O)² +(y_D-y_O)² )^½ =((4*3^½-0)² +(0-0)² )^½ = 4*3^½.
½BC * OD =16*3^½ cm².
Aire d'un des deux quadrilatère = (aire du triangle OBC- aire du triangle AEF ) /2 =(16*3^½ -(8*3^½ -6))/2 =4*3^½ +3 cm².

Quelle est la forme exponentielle du complexe z = -5 +5i ?
Module de z : ((-5)² +5²)^½ =50^½ =5*2^½ ; argument de z : arctan( 5/(-5) = -p/4.
Par suite z = 5*2^½ e(-ip/4).

z₁ =2*2^½e^(3ip/4) et z₂ =2^½e^(-ip/3). Quel est le module et l'argument du produit z₁ z₂ ?
Faire le produit des modules (2*2^½ *2^½=4) et la somme des arguments (3p/4-p/3=9p/12-4p/12=5p/12 ).

Ecrire plus simplement le nombre complexe suivant :

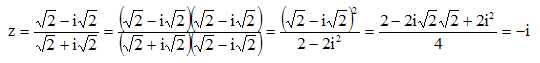
Quelle est la forme algébrique du complexe de module 2*3^½ et d'argument 2p/3 ?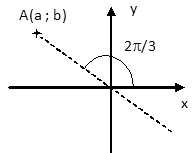
z =a+ib avec tan (2p/3) = b/a = -3^½ et (a²+b²)^½ =2*3^½ ;
b = -3^½a ; (a²+( -3^½a)²)^½ = (a²+3a²)^½ =(4a²)^½ =±2a =2*3^½ ; a = ±3^½ ; on retient a = -3^½, d'après le schéma.
par suite b = -3^½a = + 3 et z = -3^½ +3i.

.

menu