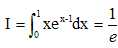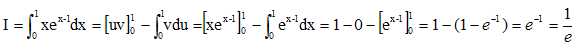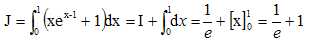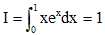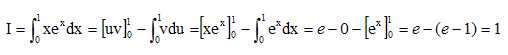Calcul
d'aire, fonction exponentielle,
bac.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Soit
f la fonction définie sur [0; 1] par f(x) = xex.
On désigne par C la courbe représentative de f dans le plan muni d’un
repère orthogonal (O, i, j).
Soit a un nombre réel appartenant à l’intervalle [0; 1].
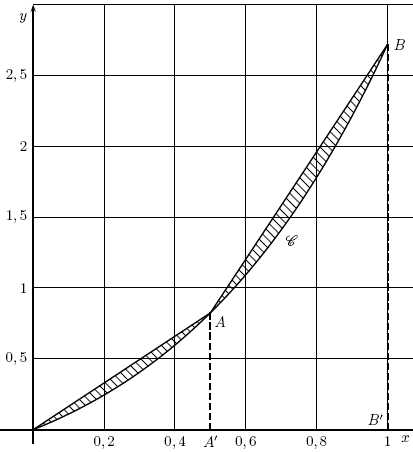
Sur la courbe C , tracée ci-dessous, on a placé les points A et B
d’abscisses respectives a et 1. On a tracé les segments [OA] et [AB].
On a hachuré la partie du plan délimitée par les segments [OA] et [AB]
et la courbe C. On a placé les points A'(a; 0) et B'(1; 0).
Le but de l’exercice est de déterminer la valeur du nombre réel a pour
laquelle l’aire de la partie du plan hachurée est minimale.
|
|
|
Partie
A :
Montrer que :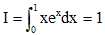
On pose u = x et exdx = dv ; v = ex
et dx = du.
Les fonctions u et v sont dérivables sur [0 ; 1] ; de plus u' et v'
sont continues sur [0 ; 1 ], on peut effectuer une
intégration par
parties :
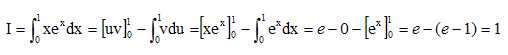
Donner
l’aire du triangle OAA' et montrer que l’aire du trapèze ABB'A' est
égale à : ½(-a2ea+aea-ae+e)
Aire du triangle OAA' : ½OA' x AA' =½a aea =½a2ea.
Aire du trapèze : ½(AA'+BB') x A'B'.
AA' = a ea ; BB' =e ; A'B' = 1-a.
Par suite : ½(a ea+e)(1-a) =½(-a2ea+aea-ae+e).
En déduire
que l’aire de la partie du plan hachurée est :
½(a ea -ae + e-2).
Aire du triangle OAA' + aire du trapèze ABB'A' - aire I
½a2ea
+½(-a2ea+aea-ae+e)
-1 =½(a ea
-ae + e-2).
|
| .
. |
.
|
|
Partie
B.
Soit g la fonction définie sur [0,+oo[ par g(x) = x(ex−
e) + e − 2.
Soit g' la fonction dérivée de la fonction g. Calculer
g'(x) pour tout réel x de [0;+oo[.
La dérivée de la constante e-2 est nulle ; on pose u = x et v =ex-e
; u' = 1 et v' = ex.
Dérivée d'un produit : g'(x) =u'v
+ v'u = ex− e + xex.
Vérifier
que la fonction dérivée seconde g" est définie sur [0;+oo[ par g"(x)
= (2+x)ex.
g"(x) =ex+ex
+xex =ex(2+x)
En déduire
les variations de la fonction g' sur [0;+oo[.
Pour x appartenant à l'intervalle [0 ; +oo[, g"(x) est positive : g'(x)
est strictement croissante sur cet intervalle.
Établir
que l’équation g'(x) = 0 admet une solution unique a dans
l’intervalle [0;+oo[. Déterminer une valeur approchée de a à 10−1 près.
g'(0) =e0(1+0)-e =1-e. Quand x tend vers
l'infini, xex et ex
tendent vers l'infini.
g'(x) est continue et strictement croissante sur [0 ; +oo [.
De plus 1-e est négatif, donc zéro appartient à l'intervalle [1-e ; +oo
[ : g'(x) =0 admet une seule solution.
g'(0,5) = 1,649 -2,718 +0,824 = -0,244.
g'(0,6) =1,82 -2,718 +1,09 =0,19. a
est compris entre 0,5 et 0,6.
En
déduire les variations de la fonction g sur [0;+oo[.
g'(x) est négative sur [0 ; a
[ : g(x) est décroissante sur cet intervalle.
g'(x) est positive sur ]a
; +oo[ : g(x) est croissante sur cet intervalle.
g'(x) =0 pour x = a
: g(x) possède un minimum pour x =a.
En utilisant les réponses aux questions des parties A et B, montrer
qu’il existe une valeur de a pour laquelle l’aire de la partie du plan
hachurée est minimale. Donner cette valeur de a.
L'aire du plan
hachurée est égale à : ½(a ea
-ae + e-2), c'est à dire ½g(a).
De plus
g(x) possède un minimum pour x
=a.
L'aire
hachurée
est donc minimale pour x =a.
|
On
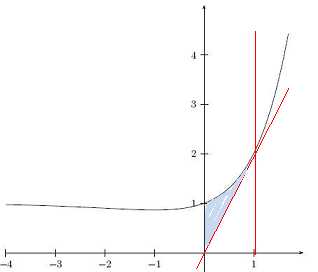
considèrela fonction f définie sur R : f(x) = xex-1+1
et on note C sa courbe représentative.
Etude
de la fonction.
Déterminer
la limite de f en −oo. Que peut-on en déduire pour la courbe C
?
L'exponentielle ex-1 tend rapidement vers zéro
quand x tend vers -oo ; xex-1
tend donc vers zéro.
f(x) tend vers 1 lorsque x tend vers -oo.
La droite d'équation y = 1 est asymptote à la courbe.
Déterminer
la limite de f en +oo.
L'exponentielle
ex-1 tend rapidement vers l'infini quand x tend
vers +oo ; xex-1
tend donc vers l'infini.
f(x)
tend vers +oo lorsque x tend vers +oo.
On admet
que f est dérivable sur R et on note f" sa fonction dérivée.
Montrer
que, pour tout réel x, f"(x) = (x + 1)ex−1.
On pose u = x et v =ex-1 ; u' = 1 et v' = ex-1.
Dérivée d'un produit : f'(x) =u'v + v'u = ex-1 +xex-1 = (1+x)ex-1.
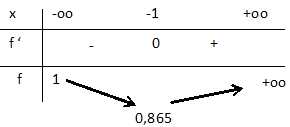
Étudier
les variations de f sur R et dresser son tableau de variation sur R.
L'exponentielle est toujours positive ;
f '(x) est négative si x < -1 : f(x) est décroissante
sur ]-oo ; -1[.
f
'(x) est positive si x > -1 : f(x) est croissante sur
]-1 ; +oo1[.
f '(x) = 0
pour x = -1. f(x) possède un minimum pour x = -1.
Recherche
d’une tangente.
Soit a un réel strictement positif. Le but de cette partie est de
rechercher s’il existe une tangente à la courbe C au point d’abscisse
a, qui passe par l’origine du repère.
On appelle T la tangente à C au point d’abscisse a. Donner une
équation de T.
L'équation de la tangente est de la forme y = ax +ß avec a =f '(a) =(1+-a)ea-1.
Au point de tangence : f(a) =(1+a)ea-1a +ß =
aea-1+1.
ß = aea-1+1 -a(1+a)ea-1 = -a2ea-1+1 ; par suite l'équation de T est y =(1+a)ea-1x -a2ea-1+1.
Démontrer
qu’une tangente à C en un point d’abscisse a strictement positive passe
par l’origine si et seulement si a vérifie l’égalité : 1 −
a2ea−1 = 0.
Si la tangente passe par l'origine ß =0 soit 1 − a2ea−1
= 0.
Démontrer
que 1 est l’unique solution sur l’intervalle ]0,+oo[ de l’équation 1 − x2ex−1 = 0.
1-12e1-1=1-1 e0
= 1-1 = 0 : 1 est bien solution de l'équation 1 − x2ex−1
= 0.
x2ex−1
-1=0 peut s'écrire x2-e1-x
=0
On pose g(x) = x2-e1-x
; g'(x) =2x+e1-x ; sur ]0 ;
+oo[, g'(x) est strictement positive : g(x) est strictement croissante
sur cet intervalle.
g(0,01) ~ -0,37 ; g(x) tend vers l'infini lorsque x tend vers l'infini.
Donc x=1 est l'unique solution de 1 − x2ex−1
= 0 sur l'intervalle ]0 ; +oo[.
Donner une
équation de la tangente recherchée.
ß est nul si a = 1 ; par suite l'équation de la tangente à C passant
par l'origine est : y =(1+1)e1-1x= 2x.
|
.
|