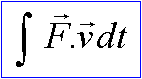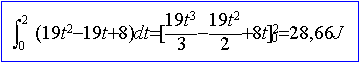Aurelie novembre 2000

. .
travail et puissance

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.

1

puissance

travail

Une particule se déplace dans un champ de forces

Suivant la trajectoire définie par les équations paramétriques, dans le système des unités SI:

x=3t ; y=2t2 ; z=t-2

  1. Calculer la puissance reçue par la particule à l'instant t.
  2. Quelle est la position de la particule lorsque cette puissance est minimale?
  3. Calculer le travail fourni par le champ de forces entre les instants t1=0s et t2= 2s?
  4. Quel est ce travail si la particule est astreinte à se déplacer en ligne droite de sa position à l'instant t1=0 à sa position à l'instant t2=2s? Conclusions?

 

corrigé


puissance :

z-x = t-2 -3t = -2-2t ;

2z²-x = 2(t-2)²-3t = 2t²-11t + 8

vecteur force (25t²/3 ; -2-2t ; 2t²-11t + 8 )

vecteur vitesse : dérivée du vecteur position par rapport au temps

( 3 ; 4t ; 1)

puissance : produit scalaire entre vecteur force et vecteur vitesse

P= 12,5 *2t² + (-2-2t)*4t + 2t²-11t + 8

P= 19t² -19t +8

la puissance passe par une valeur extrème (mini ou maxi) lorsque sa dérivée par rapport au temps est nulle ; soit 38t-19 =0 ou t= 0,5 s

à t < 0,5 s, la dérivée est négative donc la puissance diminue, passe par un minimum à t=0,5 s puis croît pour t>0,5 s.

position de la particule à t=0,5 s :

x= 3*0,5 = 1,5 ; y= 2*0,5² = 0,5 ; z= 0,5-2 = -1,5.

travail entre t = 0 et t = 2s :

si le déplacement s'effectue suivant un segment de droite AB, le travail est égal à :

coordonnées de A ( position initiale à t=0) : (0 ; 0 ; -2)

coordonnées de B (position finale à t=2) : (6 ; 8 ; 0)

vecteur déplacement : (6 ; 8 ; 2 )

vecteur force (25t²/3 ; -2-2t ; 2t²-11t + 8 )

travail = produit scalaire vecteur force par vecteur déplacement :

50 t²+8(-2-2t)+2*(2t²-11t + 8 ) = 50 t2-38 t

à t= 2 s, ce travail est égal à : 140 J

le travail dépend du chemin suivi, les deux valeurs du travail étant différentes entre t=0 et t=2 s.

La force n'est pas conservative.

retour - menu