Aurelie mai 2001

. .
suspension d'un véhicule

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.

1

oscillations

amortissement

 
  1. La suspension d'une voiture automobile, de masse M=600kg est schématisé par un ressort de raideur k. On constate que les roues, dont on négligera la masse, quittent le sol lorsque la voiture est soulevée d'une hauteur h=30cm. Déterminer:
  2. La raideur k du ressort.
  3. L'équation du mouvement verticale, ainsi que la période des oscillations verticales de la voiture à vide.
  4. Que devient la période avec 4 passagers de masse totale m=300kg.
  5. On ajoute à la suspension précédente un amortisseur qui crée une force de frottement proportionnelle à la vitesse verticale f = -bv.
    A vide, le régime d'amortissement est critique. Ecrire l'équation du mouvement vertical. Déterminer b.
  6. Lorsque la voiture contient 4 passagers, quelles sont

    - l'équation du mouvement vertical.

    - La pseudo-période T', la comparer à la période propre de l'oscillation non amortie.

    On donne g=10m.s-2. 

corrigé


raideur du ressort :

poids du véhicule : 600*10 = 6000 N

hauteur : h=0,3 m

raideur k= 6000 / 0,3 = 2 104 N/m.

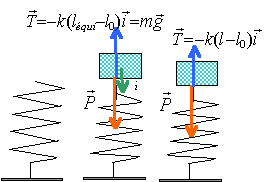
période :

l'extrémité supérieure du ressort est soumise au poids du véhicule et à la tension du ressort.

la relation fondamentale de la dynamique s'écrit : mz"= mg -k(l-l0)

l'origine est choisie à la position d'équilibre : l = léqui+ z

k(l-l0 )= k(léqui-l0 + z ) = mg + kz

par suite : mz"= -kz ou z" + k/m z =0.

les solutions de cette équation différentielle sont de la forme z = A cos (w0t+j) et le mouvement est sinusoidal de pulsation w0= racine carrée (k/m) = (2 104 / 600) 0,5 = 5,77 rad /s.

la période vaut : T0= 2p / w0 =6,28 /5,77 = 1,088 s.

avec 4 passagers la pulsation devient : (2 104 / 900) 0,5 = 4,714 rad /s. et la période : 1,33 s.

amortissement régime critique:

l'équation différentielle ci dessus s'écrit : z" -b/m z' + k/m z =0

équation caractéristique : r² -b/m r + w0 ² =0

discriminant : D =(b/m)²-4w0 ² ;

régime critique D=0 d'où b²= 4km et b=2 racine carrée(20000*600)= 6928 kg /s.

amortissement régime pseudopériodique :

D =(b/m)²-4w0 ² = 4[(b/(2m))²-4w0 ² ]

le discriminant de l'équation caractéristique est négatif si m est égal à 900kg au lieu de 600kg

le mouvement est sinusoïdal amorti de pseudo pulsation w telle que :

w² = w0 ² -(b/(2m))² = 4,714²-(6928/1800)² =22,22-14,81 = 7,41

w = 2,72 rad/s et la pseudo période T ' vaut 6,28/2,72 = 2,3 s

retour - menu