aurélie 04/2000 thermodynamique BTS EEC - bâtiment

BTS EEC, TP : thermodynamique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


1
cours classique

PV=nRT gaz parfait

P pression en pascal

V volume en m3

n moles

R=8,31 Jmol-1K-1

T en kelvin

DU =Cv DT

la variation d'énergie interne (joule) d'un gaz parfait ne dépend que de la variation de température.

Cv capacité thermique à volume constant J K-1

T en kelvin

Cp-Cv=nR

Cp capacité thermique à pression constante J K-1

transformation adiabatique PVg =constante g=1,4

l'énergie échangée avec l'extérieur est nulle

le travail échangé avec l'extérieur est égal à DU

transformation isobare La pression reste constante

l'énergie échangée avec l'extérieur est Cp DT

le travail échangé avec l'extérieur est égal à -P DV

transformation isochore le volume reste constant

l'énergie échangée avec l'extérieur est DU

le travail échangé avec l'extérieur est nul

transformation isotherme la température reste constante

l'énergie interne ne varie pas

 

retour - menu

2
1er sujet (EEC 99 -7 points)

données: Cv=20,8 J mol-1 K-1 ; CP=29,12 J mol-1 K-1 ; R = 8,31 J mol-1 K-1

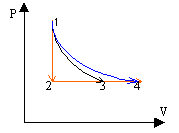
Un gaz parfait peut subir différentes transformations réversibles pour passer de l'état initial (1) au même état final (4):

  • (a) une transformation isotherme
  • (b) une transformation isochore, suivie d'une transformation isobare
  • (c) une transformation adiabatique, suivie d'une transformation isobare
  1. Quelles sont sur la figure, les courbes représentant chacune de ces transformations?
  2. les différents états du gaz sont décrits dans le tableau ci-dessous
    paramètres
    etat 1
    état 2
    état 3
    état 4
    pression (Pa)
    1,6 105



    0,8 105
    volume (L)
    80



    160
    température (K)
    300


    246


    Calculer la quantité de matière concernée par ces transformations. Compléter le tableau ci-dessus
  3. Calculer la valeur du travail reçu par le gaz au cours des transformations (1) -->(2) et (2) -->(4)
  4. Calculer la quantité de chaleur reçue par le gaz au cours des transformations (1)-->(3), (1)-->(2) et (2) -->(4)
  5. Calculer la variation d'énergie interne du gaz quand il passe de l'état (1) à (4).
corrigé

courbe (1) à (2) : isochore et courbe (2) à (4) isobare : transformation b

courbe (1) à (3) adiabatique et courbe (3) à (4) isobare : transformation c

courbe (1) à (4) isotherme : transformation a.

quantité de matière en mole

n = P1 V1 /(RT1) = 1,6 105*0,08 /(8,31*300)

n= 5,13 mol

pression (2) = pression (3) = pression (4) isobare

volume (1) = volume (2) isochore

T (4) =T (1) isotherme

T2 = P2 V2 / (R n) =0,8 105*0,08/(8,31*5,13)

T2 = 150 K

(1)-->(3) adiabatique : P1 V1g =P3 V3g

1,6 105*0,081,4 = 0,8 105 V31,4

V3 = 131 L

travail et chaleur échangés

transformation (1) -->(2) : pas de travail, car volume constant

transformation (2) -->(4) : isobare

travail échangé : - P2( V4-V2) = -0,8 105*0,08 = -6,4 kJ.

transformation (1) -->(3) : pas de chaleur échangée car adiabatique.

transformation (1) -->(2) : Q= n Cv (T2-T1)

5,13*20,8*(-150) = -16 kJ.

transformation (2) -->(4) : Q= n CP (T4-T2)

5,13*29,12*150 = 22,4 kJ.

transformation (1) -->(4) : isotherme donc pas de variation d'énergie interne.

 

retour - menu

3
Travaux Publics 1997

 

  1. Ecrire la loi (équation d'état) des gaz parfaits. Indiquer le nom et l'unité de chaque grandeur.
  2. Une bouteille de dioxygène O2 de contenance 10 litres, contient ce gaz supposé parfait, à la pression de 200 bars et à la température de 20° C.
    Calculer le nombre de moles de molécules de dioxygène contenues dans cette bouteille.
    Calculer, la masse de gaz contenue dans la bouteille.
    La température est portée à 30°C. Nommer la transformation effectuée. Que peut-on dire du nombre de moles de gaz contenues dans cette bouteille ? Calculer alors la nouvelle pression dans la bouteille.
  3. On enlève du gaz de la bouteille pour ramener la pression dans la bouteille à 200 bars, la température restant est égale à 30°C. Nommer la transformation effectuée.
    Calculer le nombre de moles de gaz extrait.
    Calculer le volume de gaz enlevé de la bouteille?, mesuré à 30° C et 1 bar.

Données

Constante des gaz parfaits : R= 8,31 J.mol-1. K-1.

Masse molaire atomique : 0 =16g.mol-1.

corrigé

PV= nRT gaz parfait

P pression en pascal ; V volume en m3 ; n moles ; R=8,31 Jmol-1K-1 ; T en kelvin

volume : 10 L=0,01 m3; presion P= 200 bars = 200 105 Pa ; T= 273+20= 293 K

n = PV / (RT) = 200 105 *0,01 / (8,31*293) = 82,14 mol

masse molaire O2 : 16*2 =32 g/mol

masse de gaz : 82,14*32 = 2628,5 g.

La température augmente, le volume de la bouteille reste inchangé: la pression du gaz va augmenter (compression)

La quantité de matière (mol) de gaz ne change pas ( pas d'ouverture de la bouteille)

nouvelle pression P2 :

P2 = nRT2 / V = 82,14*8,31*(273+30) / 0,01 = 206,82 105 Pa = 206,82 bars

la température ne change pas, le volume de la bouteille ne change pas, la pression diminue (détente du gaz), la quantité de matière du gaz diminue

T2=273+30=303K; V=0,01 L; P=200 105 Pa

n2 = 200 105*0,01 /(8,31*303) = 79,43 mol

soit 82,14-79,43 =2,71 mol de gaz extrait.

volume du gaz extrait :

T2=273+30=303K; P= 105 Pa ; n= 2,71 mol

V= nRT2 / P = 2,71 *8,31*303 / 105 =6,82 10-2 m3 = 68,2 L.

 

retour - menu