Il faut faire la somme des amplitudes des ondes
émises par chaque élément diffractant
de l'ouverture (les sources secondaires étant
cohérentes entre elles). Ensuite pour obtenir
l'intensité lumineuse I(M) il faudra élever au
carré.
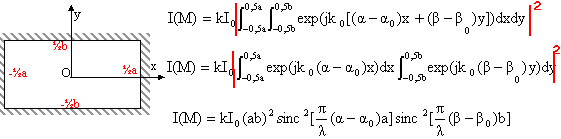
I0 : intensité de la source
k0 =
2p/l
u : vecteur d'onde ( les
vecteurs sont écrits en bleu et en gras )
u : vecteur unitaire
( cosinus directeurs a, b) pour
la direction incidente
u' : vecteur unitaire
( cosinus directeurs a',
b') pour la direction diffracté.
La figure de diffraction est formée d'une tache
centrale brillante ( intensité I0)
encadrée de taches latérales beaucoup moins
éclairées, séparées par des
zones noires.
maximum principal ( tache centrale) : a
= a ' et b
=b' directions incidente
et diffractée sont identiques.
minimums nuls : soit a
- a ' = pp
ou b -b'
= qp , p et q entiers positif ou
négatif différents de zéro.
maximums secondaires : sinc² (p/l(a-a')
= sinc² u est maximum ; cela correspond à u= tan
u.
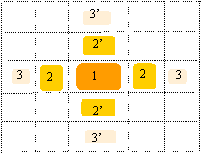
la frange centrale a une largeur double des franges
latérales ( dans les interférences les franges
ont même largeur et même éclairement).
L'éclairement des franges latérales va
décroissant.
(1) : intensité I0 ; (2 et 2')
:intensité 0,047I0 ; (3 et 3') :
intensité 0,017 I0.
dans le cas d'une fente isolée, la longueur b est
très grande devant la largeur a. ( a restant de
l'ordre de grandeur de l)
il y aura diffraction uniquement dans la direction Ox de
la largeur.
Ce résultat ne s'applique pas lorsqu'il y a
plusieurs fentes ( réseau, fentes d'Young) : il faut
sommer les amplitudes et non pas les intensités
lumineuses ( proportionnelles au carrée de
l'amplitude)