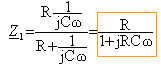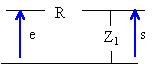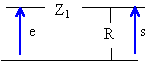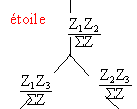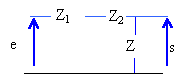Aurélie mars 2001

. .
fonction de transfert

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.

1

.

On considère un quadripôle alimenté par une tension alternative sinusoïdale. Déterminer la fonction de transfert définie par s / e. ( s et e sont des nombres complexes). On admet que le circuit d'utilisation a une impédance infinie.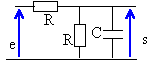

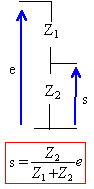corrigé

On associe à chaque grandeur physique un nombre complexe. On peut alors appliquer les règles habituelles du courant continu aux nombres complexes.

Z1 : impédance complexe équivalente à la résistance et au condensateur montés en dérivation

circuit équivalent :

diviseur de tension :

s = Z1 / (R+Z1) e = 1 / 1+R/Z1) e

fonction de transfert H = 1 / (2 +jRCw)
2

.

On considère un quadripôle alimenté par une tension alternative sinusoïdale. Déterminer la fonction de transfert définie par s / e. ( s et e sont des nombres complexes). On admet que le circuit d'utilisation a une impédance infinie.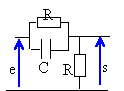

corrigé


On associe à chaque grandeur physique un nombre complexe. On peut alors appliquer les règles habituelles du courant continu aux nombres complexes.

Z1 : impédance complexe équivalente à la résistance et au condensateur montés en dérivation

circuit équivalent :

diviseur de tension :

s = R/ (R+Z1) e = 1 / 1+Z1/R) e

fonction de transfert H = (1+jRCw) / (2 +jRCw)
3

.

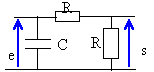
On considère un quadripôle alimenté par une tension alternative sinusoïdale. Déterminer la fonction de transfert définie par s / e. ( s et e sont des nombres complexes). On admet que le circuit d'utilisation a une impédance infinie.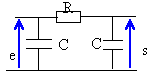

 

même question avec

corrigé


On associe à chaque grandeur physique un nombre complexe. On peut alors appliquer les règles habituelles du courant continu aux nombres complexes.

le diviseur de tension donne :

s = [1/jCw] / (R+1/jCw) e = 1/ (jRCw+ 1) e

fonction de transfert H =1/ (jRCw+ 1)

le diviseur de tension donne :

s =R / (2R) e

fonction de transfert H = 1/ 2
4

transformation de Kenelly

On considère un quadripôle alimenté par une tension alternative sinusoïdale. Déterminer la fonction de transfert définie par s / e. ( s et e sont des nombres complexes). On admet que le circuit d'utilisation a une impédance infinie.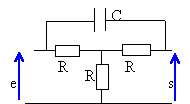

rappel

corrigé


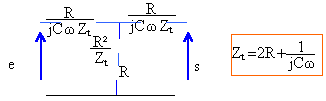
diviseur de tension (impédance de sortie infinie):

s = (R+R²/ Zt] / [R + R²/ Zt+ R/(jCw)] e

fonction de transfert : H= ( R+Zt) / [Zt+R+1/(jCw)]

remplacer Zt par son expression :

H= (1+3jRCw) / (2+3jRCw)

 
5

.

On considère un quadripôle alimenté par une tension alternative sinusoïdale. Déterminer la fonction de transfert définie par s / e. ( s et e sont des nombres complexes). On admet que le circuit d'utilisation a une impédance infinie.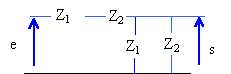

Préciser cette fonction dans les cas suivants :

  1. le dipôle (1) est une résistance et le dipôle (2) un condensateur.
  2. le dipôle (1) est une résistance et le dipôle (2) une inductance.
  3. le dipôle (1) est un condensateur et le dipôle (2) une inductance.
corrigé


On associe à chaque grandeur physique un nombre complexe. On peut alors appliquer les règles habituelles du courant continu aux nombres complexes.

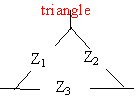
Z inductance équivalente à Z1 et Z2 en dérivation :

Z = Z1 Z2 / (Z1+Z2)

circuit équivalent :

le diviseur de tension donne :

s = Z / (Z1+Z2+Z) e

fonction de transfert : H = 1 / [(Z1+Z2) / Z +1]=1 / [(Z1+Z2)² / (Z1 Z2) +1]

Z1=R et Z2= 1 / (jCw) :

Z1+Z2= R+1 / (jCw) =(jRCw+1) / (jCw) et Z1 Z2= R/ (jCw)

et (Z1+Z2)² / (Z1 Z2) =(jRCw+1)²/ (jRCw ) = 2 + j[RCw-1/(RCw)].

H= 1 / {3 + j[RCw-1/(RCw)]}.

Z1=R et Z2= jLw :

Z1+Z2= R+jLw et Z1 Z2= jRLw.

et (Z1+Z2)² / (Z1 Z2) =( R+jLw)²/ (jRLw ) = 2 + j[Lw/ R- R /(Lw)].

H= 1 / {3+ j[Lw/ R- R /(Lw)]}.

Z1=1 / (jCw) et Z2= jLw :

Z1+Z2= 1 / (jCw) +jLw et Z1 Z2=L / C

et (Z1+Z2)² / (Z1 Z2) = -( Lw-1/(Cw))² *C / L = 2-(LCw²+ 1/ (LCw²)

H= 1 / {3-(LCw²+ 1/ (LCw²)}.

retour - menu