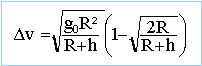Aurélie fevrier 2001

. .
mouvement dans un champ newtonien

révision : les coniques

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.

1

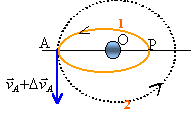
orbite circulaire

orbite elliptique

Un solide ponctuel de masse m est lancé depuis la terre avec une vitesse initiale v0 formant un angle a avec la verticale. La Terre de masse M>>m est en conséquence immobile. Ce solide décrit une ellipse (grand axe 2a) dont l'un des foyers est le centre de la Terre. A son apogée, notée A sa vitesse est vA ; on lui communique alors pendant un laps de temps très court une force constante tangente à l'orbite. La vitesse augmente sans que la position change.

  1. La nouvelle orbite étant circulaire de rayon r =R+h ( h : altitude comptée depuis le sol), exprimer la variation de vitesse en fonction de R, h, a, v0 et g0.
  2. On applique à nouveau une force constante, tangente à l'orbite, pendant un laps de temps t très court. Il y a un brusque changement de vitesse sans changement de position. La nouvelle orbite est une ellipse. Déterminer ces paramètres ( a: demi grand axe et e excentricité) en fonction de R et h afin que rPérigée=R. Expression de l'énergie totale sur une orbite elliptique : E= -GMm/(2a).
  3. Déterminer le sens et la norme de F en fonction de t, m, R, h et g0.
corrigé


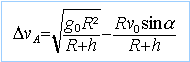
ancienne orbite :

Le vecteur accélération passe par le point fixe O:

le moment cinétique est constant égal au départ à L = mR v0 sina.( R rayon terrestre)

et égal à L= m rAvA sur l'ellipse en A. (rA=R+h)

loi de aires : la vitesse aérolaire est constante r²q' = C = L / m = cte

vA= C / rA= R v0 sina / (R+h).

nouvelle orbite circulaire :

relation fondamentale de la dynamique suivant l'axe n de la base de Frenet

GMm / (R+h)² = mv²/ (R+h) avec GM=g0R²

v²= g0R² / (R+h)

l'ancienne orbite est circulaire de rayon R+h, la nouvelle orbite esr elliptique de périgée R.

La partie commune est l'apogée de la nouvelle orbite.

nouvelle orbite elliptique :

apogée : R+h; périgée : R donc 2a = 2R+h ou a = R+½h.

équation de la trajectoire en coordonnées polaires :

r = p / (1+ecosq)

rapogée = p / (1-e) et r périgée = p / (1+e) ou bien e = h / (2R+h).

l'énergie doit diminuer pour passer d'une orbite circulaire à une orbite elliptique.

énergie après freinage sur la nouvelle orbite elliptique.

-GMm / (2R+h) = ½m(v-Dv)²-GMm / (R+h)

(v-Dv)²= 2GM[ 1/(R+h) - 1/ (2R+h)] avec GM=g0R²

appliquer la relation fondamentale de la dynamique pendant la durée t du freinage

F=dp/dt =mDv / t.

retour - menu