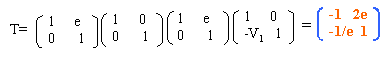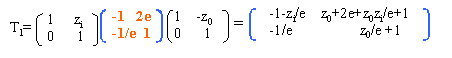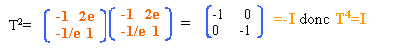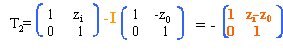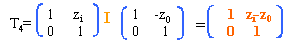|
.
. |
|
||||
|
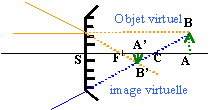
miroir convexe |
corrigé |
||||
|
|
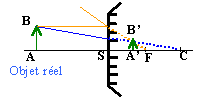
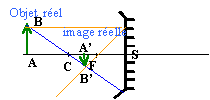
L'image étant réelle,droite, trois fois plus grande que l'objet : fig 2 ci dessus mesure algébrique SA' / mesure algébrique SA =3
|
||||
|
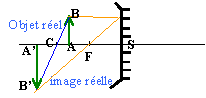
miroir concave |
corrigé |
||||
|
|
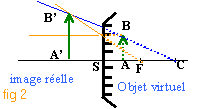
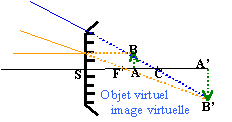
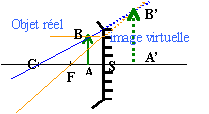
L'image étant réelle,droite, trois fois plus petite que l'objet : fig 4 ci dessus mesure algébrique SA' / mesure algébrique SA =1 /3
|
||||
|
rétroviseur |
corrigé |
||||
|
|
orientation : sens de la lumière; le sens change après réflexion formule de conjugaison et grandissement :
mesure algébrique de SC=2,2 m . Miroir convexe divergent 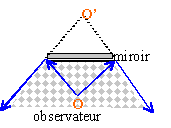
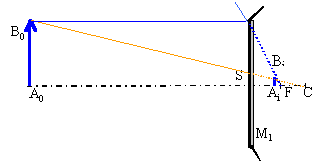
Le champ d'un miroir est la région de l'espace vue par un observateur à travers le miroir. Il est défini par le cône qui s'appuie sur le contour du miroir et dont le sommet est l'image de l'oeil de l'observateur. Ce champ augmente lorsque la distance oeil-miroir diminue. Recherchons l'image de l'oeil :
L'image est virtuelle à l'arrière du miroir, à une distance de 33,3 cm. Le rayon r du champ est : r / 0,04 =100,334 /0,334 d'où r voisin de 12 m. Avec un miroir plan l'image serait symétrique; r / 0,04 =101 /1 d'où r voisin de 4 m.
|
||||
|
cavité laser |
A l'aide de 2 miroirs, l'un M1 sphérique et l'autre M2 plan, on réalise une cavité laser hémifocale. Les surfaces réfléchissantes se faisant face, le foyer de M1 coïncide avec le sommet de M2. Exprimer la matrice de transfert entre un plan de front situé en A0 et un plan de front situé en A1 après une réflexion sur chaque miroir. 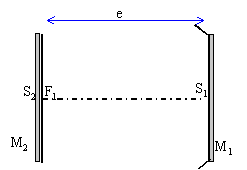
|
||||
|
|
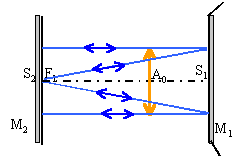
matrice de transfert pour un aller et retour - menu : vergence du miroir sphérique V=-2 / (-2e)=1/e translation S2S1, réflexion sur M2(miroir plan), translation S1S2, réflexion sur M1. matrice de transfert entre les deux plans de front après une réflexion sur chaque miroir
matrice de transfert pour deux aller et retour - menu :
Les points étant conjugués, z0=zi et le grandissement est -1. matrice de transfert pour 4 aller et retour - menu :
Les points étant conjugués, z0=zi et le grandissement transversal est +1. |
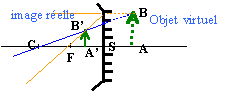 fig
4
fig
4