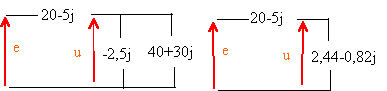|
.
. |
th. de Boucherot : S puissances absorbées par les appareils en dérivation En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Th de Boucherot puissances |
L'impédance de la ligne est assimilable à une résistance R=0,1 W en série avec une inductance L=0,1 mH. tension aux bornes de l'installation u(t) =325 sin(wt+j) tension début de ligne e(t) = 1,414 E sin(wt) avec f=50 Hz 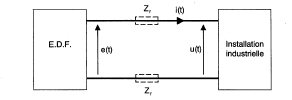 L'installation comprend : (tout fonctionne simultanément)
corrigé |
|
|
|
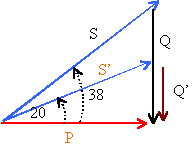
puissance apparente SL=PL=1,5 VA les 2 moteurs : P1= 6 kW; j =cos-1(0,7)=45,6°; sinj =0,714 puissance apparente S1: 6/0,7 = 8,57 kVA puissance réactive Q1 : S1 sin j = 6,12 kVAR les 6 moteurs : P1= 6*4,5 /0,9 = 30 kW; j =cos-1(0,8)=36,9°; sinj =0,6 puissance apparente S2:30/0,8 = 37,5 kVA puissance réactive Q2 : S2 sin j = 22,5 kVAR total installation : P = 37,5 kW; Q=28,62 kVAR; S² = P² + Q² d'où S =47,17 kVA facteur de puissance de l'installation: cos j = P/S = 37,5 / 47,17 = 0,795 j =cos-1 0,795 = 37,3° intensité
en ligne : I (A) = S (VA) / U(V) = 47 170 / 220 =
214,4
A.
puissance active RI² = 0,1 *216² = 4,66 kW puissance réactive Lw I² =0,0314*216²=1,465 kVAR w =2*3,14*50 =314 rad /s. Lw = 314*0,1 10-3 =0,314 W. puissances fournie par EDF : puissance active : P=37,5 + 4,66= 42,16 kW puissance réactive : Q=28,62 +1,465 = 30 kVAR puissance apparente S²= P²+Q² d'où S=51,74 kVA tension efficace E : 51 740 / 214,4
=241,3 V
la puissance active n'est pas modifiée par le branchement du condensateur P=37,5 kW j' = cos-1 0,94 = 20° et sin j' = 0,342 puissance apparente : S'=37,5 / 0,94 = 39,9 kVA puissance réactive : Q'=S' sinj' = 13,65 kVAR Q'-Q=13,65-28,62 = -14,97 kVAR capacité du condensateur : -14 970 = -CwU² soit C=14970/(314*220²) =1 mF. intensité en ligne : I'=S' / 220 =39900 / 220= 181 A nouvelles puissances absorbées en ligne : puissance active RI'² = 0,1 *181² = 3,27 kW puissance réactive Lw I² =0,0314*181²=1,03 kVAR nouvelles puissances fournie par EDF : puissance active : P'=37,5 + 3,27= 40,77 kW puissance réactive : Q''=13,65 +1,03 = 14,68 kVAR puissance apparente S²= P²+Q² d'où S=43,33 kVA tension efficace E ': 43 330 / 181 =239,4 V
|
|
|
impédance complexe puissance
|
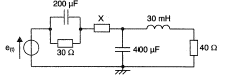
e(t) source de tension alternative de pulsation w= 1000 rad /s et de valeur efficace 21 V. 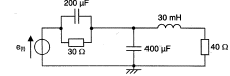
corrigé |
|
|
|
-j/(Cw): condensateur; jLw : bobine inductive
impédance complexe du dipôle : Z=22,44 -5,82j intensité complexe : i = e /Z= e(22,44+5,82j) / (22,44²+5,82²) i = e(22,44+5,82j) / 537,37 puissance complexe p= ½ e i*= ½ e²(22,44+5,82j) / 537,37 p = 0,5 (21*1,414)²/537,37 (22,44+5,82j) p = 18,41 + 4,77 j puissance active : P=18,41 W puissance réactive : Q= 4,77 VAR ajout du dipôle d'impédance X: la puissance réactive de l'ensemble est nulle : la puissance réactive du nouveau dipôle est : -4,77 VAR il 'agit donc d'un condensateur; l'ajout de ce dernier ne modifie pas la puissance active. La puissance réactive étant nulle, le facteur de puissance vaut 1; tension et intensité en phase. l'intensité efficace délivrée par la source vaut : 18,41 /21 =0,876 A capacité du condensateur : le nouveau dipôle est en série avec les impédances précédentes, l'intensité est identique à travers les diôples en série. -4,77 = -I²/ (Cw) d'où C= 1,6 10-4 F. |