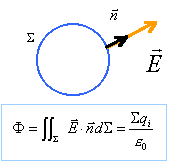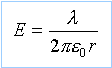|
.
. |
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|||||
|
|
|
|||||
|
champ d'une couche sphérique mince uniformément électrisé |
|
|||||
|
|
Par raison de symétrie le champ est radial.
On considère une sphère S , de centre O et de rayon x. D'après le théorème de Gauss, le flux du vecteur champ électrique à travers la surface S est nul car il n'y a pas de charge à l'intérieur de S. si x < R, le champ électrique est nul à l'intérieur de la sphère.
Soit un point M situé à une distance x > R F = E 4px² D'autre part la charge contenue à l'intérieure de S est la charge totale de la sphère de rayon R : Q = s 4pR². d'où E = s R² / (e0x²) On retrouve la discontinuité de la composante normale du champ (s / e0) à la traversée d'une surface chargée.
|
|||||
|
champ crée par une ligne uniformément chargée |
quelle est l'expression du champ crée par cette ligne ? corrigé |
|||||
|
|
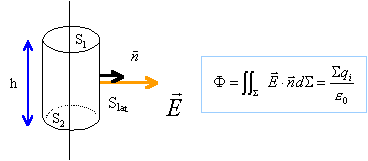
On prend comme surface S un cylindre de hauteur h , d'axe la ligne infinie, et de rayon r. En tout point de la surface latérale le champ est radial et a même module, par raison de symétrie. Le fux du champ à travers la surface latérale est : F= E 2p r h Le flux du champ est nul à travers les bases S1 et S2, le champ étant perpendiculaire à la normale aux surfaces.
l charge par unité de longueur.
|
|||||
|
|
|