Aurélie janvier 2001

. .
gaz parfaits

quelques exercices de base

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.

1

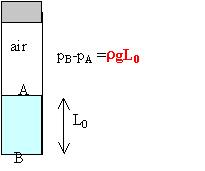
un tube plongé dans un liquide

L'air est considéré comme un gaz parfait. On plonge, à mi hauteur, un tube de verre (section s, longueur L) ouvert à ses extrémités dans un liquide de masse volumique r. On ferme l'extrémité supérieure par un bouchon étanche puis on soulève le tube hors du liquide.

  1. Exprimer la hauteur du liquide dans le tube, la pression de l'air emprisonné en fonction de r, L, g, H0, rmercure (H0 pression atmosphérique exprimée en mm de mercure).
  2. Faire les calculs pour les 2 liquides suivants : eau 1000 kg m-3 et mercure 13 600 kg m-3. L=1 m et H0 =76 cm de mercure. Exprimer la pression en pascals, en bars, en mm de mercure.
  3. Même question, on plonge le tube sur toute sa longueur.
corrigé


 

La quantité d'air emprisonné sous la pression atmosphérique reste constante.

La température reste également constante.

l'équation d'état des gaz parfaits donne :

p0 sL/2 =(p0-rgL0) s(L-L0) diviser par la section

exprimer la pression en hauteur de mercure : p0= rmercure g H0.

rmercure g H0L/2 = g( rmercure H0-rL0) (L-L0) diviser par g

rL0² -(rmercure H0-rL)L0+ rmercure g H0L/2 =0 résoudre l'équation du 2è degré en L0.

application numérique :

cas de l'eau :L0 = 0,476 m

76 cm de mercure correspond à : 0,76*13600*9,8 =1,013 105 pascals

pA = 1,013 105 -1000*9,8*0,476 = 9,66 104 pascals =0,966 bar

=9,66 104 /(9,8*13600)= 72,5 cm de mercure

cas du mercure :L0 = 0,252 m

pression : 67708 Pa ou bien 0,677 bar ou bien 50,8 cm de mercure.

Le tube enfoncé sur toute sa longueur dans le mercure, bouché puis retité constitue un tube baromètrique. La hauteur de mercure sera H0=76 cm de mercure.

Le mercure sera surmonté par du vide.

Dans le cas de l'eau, cherchons la hauteur d'eau équivalente à 76 cm de mercure :

h= 13600*0,76 / 1000 = 10,336 m d'eau

Sorti de l'eau le tube reste rempli d'eau . La pression à la partie supérieure de l'eau est 10,336-1 = 9,336 m d'eau ou 68,65 cm de mercure ou 91500 Pa.
2

mélange de trois gaz

On mélange du dihydrogène H2 (V1 =2,25 L ; p1 =0,3 bar, T1 =293 K), du diazote N2 (V2 =1,45 L ; p2 =0,8 bar, T2 =280 K) et de l'hélium (V3 =3,5 L ; p3 =0,5 bar, T3 =285 K).

masse molaire en g mol-1 H2 = 2 ; N2 = 28 ; He =4. R=8,314 J K-1 mol-1.

  1. Calculer la quantité de matière de chaque gaz (mol et masse en g) supposé parfait.
  2. On introduit les 3 gaz dans un récipient unique de volume V=6 L; lors de l'opération l'énergie interne du mélange se conserve. Calculer la température et la pression finale du mélange.
  3. Calculer la fraction molaire et la pression partielle de chaque gaz dans le mélange.
  4. Calculer la capacité thermique à volume constant savhant que pour un gaz parfait monoatomique Cv=3R/2 et pour un gaz parfait diatomique Cv=5R/2.
corrigé


Quantité de matière en mol : utiliser l'équation d'état des gaz parfaits .

exprimer les pressions en pascal : 1bar =1,013 105 Pa.

exprimer les volumes en m3 : 1 m3 =1000 L.

n1= p1V1 /(RT1) = 0,3*1,013 105 *2,25 10-3 / (8,314*298)= 0,0276 mol

de même : n2 = 0,0498 mol et n3 = 0,0739 mol

multiplier par la masse molaire (g mol-1)

m1 = 0,0276*2 =0,0554 g H2;

m2 =0,0498 *28 =1,39 g de N2 ;

m3 = 0,0739*4 = 0,265 g He.

La variation globale d'énergie interne est nulle

n1 C1v(T-T1) + n2 C2v(T-T2) + n3 C3v(T-T3) =0

C1v=C2v=2,5 R ( gaz diatomique) et C3v=1,5 R( gaz monoatomique)

(2,5 n1+2,5 n2+1,5 n3)RT = (2,5 n1T1+2,5 n2T2+1,5 n3T3)R

T=284,78 K

la quantité de matière en moles se conserve :

pV / T = p1V1 / T1 +p2V2 / T2 +p3V3 / T3

p = T/V ( p1V1 / T1 +p2V2 / T2 +p3V3 / T3 )

p=0,598 bar

fraction molaire : xi =ni / n

x1 = 0,0276 /( 0,0276 +0,0498+0,0739)= 0,18

x2 =0,33 et x3 = 0,49.

on vérifie que x1+x2+x3 est bien égale à 1.

pression partielle d'un gaz dans le mélange : pi = xi p

p1 =0,18*0,597 = 0,107 bar

p2 = 0,197 bar et p3 = 0,293 bar .

la capacité thermique à volume constant du mélange est égale à la somme des capacités thermiques à volume constant des constituants du mélange :

nCv =R(2,5 n1+2,5 n2+1,5 n3)

nCv= 2,53 J K-1.
3

mélange gaz et eau

Soit un mélange d'un gaz parfait diatomique( état initial : V1=0,1 m3; t1=27°C; p1=105 Pa) et d'eau ( 1 g ). Le volume de l'eau liquide sera négligé. La vapeur d'eau se comporte comme un gaz parfait.

  1. On effectue une compression isotherme, réversible de l'état (1) à l'état (2) telle que V2=0,01 m3. Quelle est la composition du mélange dans les 2 états considérés.
  2. On porte à partir de l'état (2), de manière irréversible le mélange à t3 =100°C. Le volume est maintenu constant. Calculer p3.
    pression de vapeur saturante : à 300K psat =3700 Pa et à 373 K psat =1,01 105Pa.
    corrigé


l'eau est-elle liquide ou gazeuse ?

pression partielle de la vapeur d'eau dans le mélange état (1) si toute l'eau est sous forme de vapeur :

peau = 1/18 *8,314 *300 /0,1=1386 Pa.

à 300 K la première goutte de liquide apparaît lorsque la pression de vapeur saturante est 3700 Pa . Donc l'eau est entièrement sous forme de gaz.

composition du mélange de gaz :

Quantité de matière d'eau sous forme de gaz : 1/18 = 0,0555 mol

Quantité totale de gaz : 0,1*105 /(8,314 *300) = 4,009 mol

Quantité de matière d'autres gaz : 3,954 mol.

même méthode pour l'état (2) avec V2=0,01 m3.

hypothèse : toute l'eau est gazeuse --> peau = 1/18 *8,314 *300 /0,01=13860 Pa.

cette valeur étant supérieure à 3700 Pa, une partie de l'eau est liquide.

Quantité d'eau gazeuse : 0,01*3700 /(8,314*300) = 0,0148 mol

soit 1-0,0148*18=0,733 g d'eau liquide.

même méthode pour l'état (3) avec T=373 K.

Quantité de matière de vapeur d'eau : 0,01 *105 /(8,314*373)= 0,322 mol

or on ne dispose que de 0,0555 mol d'eau donc toute l'eau est vapeur.

pression du mélange de gaz :

p3 =4,009*8,314*373 / 0,01 =12,43 105 Pa


à suivre ...


retour - menu


à bientôt ...