|
.
. |
d'un gaz parfait En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|||||
|
|
|
|||||
|
on brûle le fil maintenant le contre poids... |
Initialement le récipient contient de l'air ( gaz parfait) à la température T0=285 K, sous la pression P0=1 bar. La section des récipient est s=40 cm²; l0= 1m; M=50 kg; g=1,4. 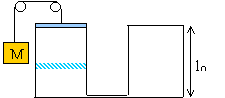
On brûle le fil maintenant le contrepoids du piston. Ce dernier se déplace vers le bas et se stabilise à la hauteur l1.
corrigé |
|||||
|
|
pression du gaz après rupture du fil La pression du gaz à l'intérieur du récipient est égale à la pression atmosphérique extérieure augmentée de la pression exercée par le poids du piston Mg sur la surface s. p1=p0+ Mg / s (1) application numérique 1,013 105+ 50*9,8 / 4 10-3 = 2,25 105 Pa=2,25 bars conservation de la quantité de matière de gaz au départ : volume V0 = 2s l0. équation d'état des gaz parfaits P0V0 = nRT0 n= P0 2sl0 /(RT0) (a) n=1,013105*4 10-3*2 /(8,31*285)= 0,342 mol à la fin : volume V1 = s(l0+l1) équation d'état des gaz parfaits P1V1 = nRT1 n= P1 s(l0+l1) /(RT1) (b) écrire (a) = (b) d'où : P0 2l0 / T0 =P1 (l0+l1) /T1. (2) la variation d'énergie interne ne dépend pas du processus DU = n Cvm (T1-T0) = We+ Qe avec Cvm = R / (g-1) pas de transfert thermique Qe=0 travail des forces de pression, poids du piston et force pressante due à l'air extérieur We= Mg(l0-l1) +P0s (l0-l1) nR / (g-1)(T1-T0)
= (Mg + P0s )(l0-l1)
(3)
additionner et simplifier
application numérique : T1=285 /1,4 *(1+0,4*2,25 ) =386,8 K repport dans (2) l0+l1 = 2 l0P0T1 / (P1 T0)=2*386,8/(2,25*285)=1,206 m l1=0,206
m
n= 0,342 mol Cvm = 8,31 / (1,4-1)= 20,775 J mol-1 K-1. DU = n Cvm (T1-T0)=0,342*20,775*(386,8-285)= 723 J variation d'enthalpie DH = n Cpm (T1-T0) Cpm = gCvm= 1,4* 20,775 = 29 J mol-1 K-1. DH = 0.342*29*(386,8-285)= 1009 J
|
|||||
|
|
|