Aurélie sept 2004 

 . .
diagramme d'Ellingham

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.

1

préparation du nickel

On étudie les réactions :

2C + O2 --> 2 CO (1) et 2 Ni + O2 --> 2 NiO (2)

  1. Tracer le diagramme d'Ellingham correspondant.
  2. En déduire un moyen de préparation du nickel.
CO
NiO
Ni
C
O2
DH0 kJ mol-1
-110,5
-244,3
0
0
0
S0 J mol-1
197,6
38
29,9
5,7
205

corrigé


calcul des DG0 :

DH01=2 DH0(CO)-2 DH0(C)-DH0(O2)= -221 kJ mol-1.

DH02=2 DH0(NiO)-2 DH0(Ni)-DH0(O2)= -488,6 kJ mol-1.

DS01=2 S0(CO)-2 S0(C)-S0(O2)= 178,8 J mol-1.

DS02=2 S0(NiO)-2 S0(Ni)-S0(O2)= -188,8 J mol-1.

DG0=DH0-TDS0

DG01 = -221 000 -178,8 T

DG02= -488 600 + 188,8 T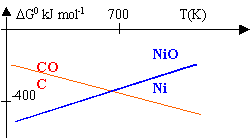

En égalisant ces 2 dernières expressions on trouve l'intersection des droites à T=728 K.

Il est donc possible de réduire NiO par le carbone au dessus de cette température, en vue de préparer le nickel.

NiO + C --> Ni + CO

A 1000 K, DG0=DG01 - DG02 = -105 J mol-1.

DG0 =-RT lnK donc K=2,3 105, réaction totale

 
2

dismutation de GeO

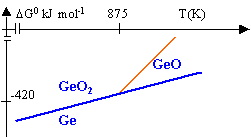
On étudie les réactions :

2Ge + O2 --> 2 GeO (1) et 2 GeO + O2 --> 2 GeO2 (2)

  1. Exprimer les DG0.
  2. Ecrire l'équilibre (3) de dismutation de GeO. Donner DG03. Etudier la dismutation en fonction de la température.
  3. Soit l'équilibre Ge + O2 --> GeO2 (4). Donner DG04.
  4. Indiquer dans quel domaine les réactions ci dessus sont envisageables.
  5. Construire le diagramme d'Ellingham pour 500<T<1000. On oxyde du germanium avec O2. Que se passe t-il à 800 K et à 950 K.
Ge
GeO
GeO2
O2
DH0 kJ mol-1
0
-255
-552
0
S0 J mol-1
21
73
77
205

corrigé


calcul des DG0 :

DH01=2 DH0(GeO)-2 DH0(Ge)-DH0(O2)= -510 kJ mol-1.

DH02=2 DH0(GeO2)-2 DH0(GeO)-DH0(O2)= -594 kJ mol-1.

DS01=2 S0(GeO)-2 S0(Ge)-S0(O2)= -101 J mol-1.

DS02=2 S0(GeO2)-2 S0(GeO)-S0(O2)= -197 J mol-1.

DG0=DH0-TDS0

DG01 = -510 000 +101 T

DG02= -594 000 + 197 T 

dismutation de GeO :

2 GeO --> GeO2 + Ge (3)

DH03= DH0(GeO2)+ DH0(Ge)-2DH0(GeO)= -42 kJ mol-1.

DS03= S0(GeO2)-2 S0(GeO)+S0(Ge)= -48 J mol-1.  

DG03 = -42 000 + 48 T

DG03 est négatif tant que T< 875 K. La constante de la réaction est supérieure à 1 et la dismutation se produit à une température inférieure à 875 K.

Ge + O2 --> GeO2 + Ge (4)

DH04= DH0(GeO2)- DH0(Ge)-DH0(O2 )= -552 kJ mol-1.

DS04= S0(GeO2)- S0(O2)-S0(Ge)= -149 J mol-1.  

DG04 = -552 000 + 149 T

point triple ( coexistence des 3 espèces) : 875 K et DG0 = -464 kJ

Avant 875 K la réaction (4 )a lieu; au dela les réactions (1) et (2) ont lieu .

à 800 K l'oxydation donne GeO2; à 950 K l'oxydation donne GeO et GeO2.


La poudre d'aluminium brûle très facilement ; la réaction est exothermique.

  1. Ecrire la réaction du dioxygène sur l'aluminium.
  2. Soit DrG°1 (T) la variation d'enthalpie standard de formation de l'oxyde d'aluminium pour la réaction de référence faisant intervenir une mole de dioxygène. Donner l'expression de DrG°1 (T) sur l'intervalle [250 K, 2500 K]. Tracer le graphe (1) correspondant .
    abscisses: 1 cm pour 125 K ; ordonnées :1 cm pour 50 kJ.mol-1
  3. Soit DrG°2 (T) l'enthalpie standard de la réaction: 2 C +O2 = 2 CO.
    -Donner l'expression de DrG°2 (T) sur l'intervalle [250 K, 2500 K]. Tracer le graphe (2) correspondant sur la même figure que le graphe (1).
  4. Le carbone peut-il réagir sur l'oxyde d'aluminium ? Si oui, à partir de quelle température la réduction de l'oxyde d'aluminium est-elle théoriquement possible ? (les conditions sont telles que le carbure d'aluminium ne se forme pas). Cette méthode est-elle utilisée ?

    Les valeurs suivantes sont considérées comme constantes dans l'intervalle de température étudié [250 K , 2500 K]
    corps
    Al(s)
    Al2O3 (s)
    C(s)
    O2(g)
    CO(g)
    CO2(g)
    S° JK-1mol-1
    28
    51
    6
    205
    197
    213
    DfH° kJ.mol-1
    0
    -1674
    0
    0
    -110
    -393
    température de fusion de l'aluminium sous 1 bar : 933 K

    enthalpie molaire de fusion de l'aluminium à 933 K: Dfusion H° = 10,9 kJ.mol-1.

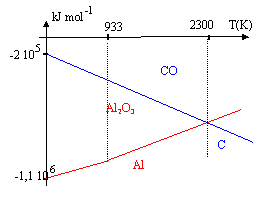
corrigé
4/3 Al + O2 = 2/3 Al2O3.(1)

sur l'intervalle [250 K, 933 K] : DH01= 2/3 DH0(Al2O3)- 4/3DH0(Al)-DH0(O2 )= -1116 kJ mol-1.

DS01= 2/3S0(Al2O3)- S0(O2)-4/3S0(Al)= 34-205-37,3 = -208,3 J K-1 mol-1.  

DG01 = -1 116 000 + 208,3 T.

sur l'intervalle [933 K, 2500 K]

DH01= 2/3 DH0(Al2O3)- 4/3[DH0(Al)+ Dfusion H°(Al)]-DH0(O2 )

DH01= -1116 -4/3* 10,9 = -1130,5 kJ mol-1.

entropie de changement d'état à 933 K :

S= Dfusion H°(Al) / Tfusion = -10900 / 933= 11,7 J K-1 mol-1.

DS01= 2/3S0(Al2O3)- S0(O2)-4/3[S0(Al)+11,7]= 34-205-53 = -224 J K-1 mol-1.

DG01 = -1 130 500 + 224 T.

2C+O2 = 2CO (2)

DH02=2 DH0(CO)-2 DH0(C)-DH0(O2)= -220 kJ mol-1.

DS02=2 S0(CO)-2 S0(C)-S0(O2)= 177 JK-1 mol-1.

DG0=DH0-T DS0

DG02= -220 000 - 177 T 

Le cabone peut réduire l'alumine si l'enthalpie libre de la réaction suivante est négative :

3C+ Al2O3 = CO + 2Al

obtenue à partir de 1,5 *(2) -1,5 (1)

DG0= 1,5(DG02 - DG01)

pour trouver la température à partir de laquelle cette réduction est possible , écrire que DG0 =0

soit DG02= DG01; -1 130 500 + 224 T= -220 000 -177 T

T= 910500/ 401 = 2270 K.

température trop élevée pour que cette méthode soit bon marché ; la préparation de l'aluminium se fait par électrolyse.


A diverses températures T, on relève les valeurs correspondantes des enthalpies libres standard DrG0 (DrHG0 et DrSG0 seront considérées indépendantes de T ) relatives aux réactions d'obtention des oxydes de cuivre (I) et (II) : Cu2O (réaction 1) et CuO (réaction 2). ( les réactions ne font intervenir qu'une mole de dioxygène ).
T (K)
300
800
1300
DrG01 kJ mol-1
-300
-230
-160
DrG02kJ mol-1
-260
-170
-80
 

  1. Représenter graphiquement les variations de DrG01 et DrG02 en fonction de T.
    Echelle : en abscisse 1 cm pour 100 K ( domaine de 0 à 1500 K)
    en ordonnée 1 cm pour 20 kJ/mol ( domaine de 0 à - 500 kJ/mol )
  2. Expliquer le signe des pentes des droites obtenues.
  3. Calculer les valeurs respectives de DrH ° et DrS° pour les réactions (1) et (2).
  4. Ecrire l'équilibre (3) de dismutation de l'oxyde de cuivre (I) en oxyde de cuivre (II) et en cuivre métal. 
  5. Exprimer la loi de variation de Dr G°3 en fonction de T.
  6. Conclure que l'existence simultanée des trois solides est impossible. Conclure sur la dismutation de Cu20
corrigé
Quand la température augmente de T=500 K, DrG01 augmente de 70 kJ/mol :

DrG01 = 70/500 T + constante = 0,14 T + constante

constante = -230 -0,14*800 = -230 -112 = - 342 kJ/mol

DrG01 = 0,14 T -342.

Quand la température augmente de T=500 K, DrG02 augmente de 90 kJ/mol :

DrG02 = 90/500 T + constante = 0,18 T + constante

constante = -170 -0,18*800 = -170 -1442 = - 314 kJ/mol

DrG02 = 0,18 T -314.

le signe positif des pentes des droites obtenues indique des réactions endothermiques.

valeurs respectives de DrH ° et DrS° pour les réactions (1) et (2).

DrG0 = DrH ° -TDrS0

par identification : DrH0 1 = -342 kJ/mol ; DrS0 1 = 0,14 kJ K-1 mol-1.

par identification : DrH0 2 = -314 kJ/mol ; DrS0 2 = 0,18 kJ K-1 mol-1.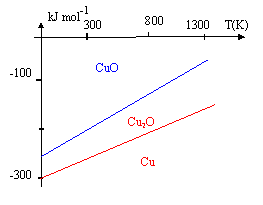

4Cu+O2 =2 Cu2O (1)

2 Cu + O2 = 2 CuO (2)

½ (2)- ½ (1) donne : Cu2O = Cu + CuO (3)

DrG03 =½(DrG02 -DrG01 )= 0,18T-314 -(0,14 T-342)

DrG03 = 0,04 T +28 .

L'étude thermodynamique de l'oxydation du cuivre montre que la coexistence, à l'équilibre, entre le cuivre et l'oxyde de cuivre (II) est impossible. L'oxyde en contact avec le métal est Cu2O. Ce dernier peut être oxydé à son tour en CuO par le dioxygène. D'un point de vue cinétique, l'oxydation du cuivre par O2 sec en CuO via Cu2O est très lente.


Réduction de la chromite:

La chromite est oxydée, en milieu alcalin, en chromate de potassium et oxyde ferrique. Le chromate de potassium est séparé par dissolution dans l’eau puis précipité sous forme de dichromate de potassium qui est réduit par le carbone en oxyde de chrome (III) Cr2O3 qu’il s’agit de réduire en chrome métallique.

  1. Le premier réducteur utilisé pour réduire l'oxyde de chrome(III) fut le dihydrogène.
    - Ecrire l'équation de la réaction de réduction d’une mole de Cr2O3 par H2 à 1300 K.
    - Calculer l’enthalpie standard, l’entropie standard et l’enthalpie libre standard de cette réaction à 1300 K.
    - Préciser l’influence de la température sur cet équilibre.
    - Exprimer et calculer la constante associée à cet équilibre à 1300 K. Conclure.
  2. Le réducteur actuellement utilisé est l’aluminium.
    Le diagramme d’Ellingham des systèmes Cr2O3 / Cr et Al2O3 / Al est fourni.

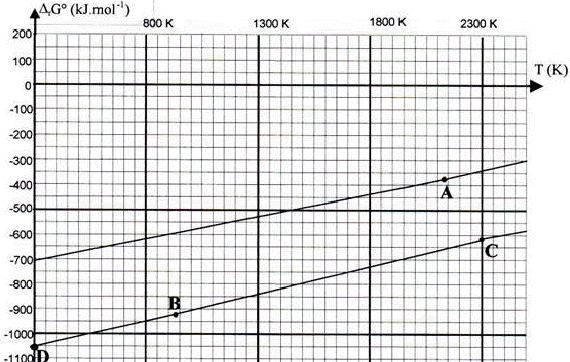Ce diagramme représente l’enthalpie libre standard de formation des oxydes pour une mole de dioxygène en fonction de la température.
- Écrire les équations donnant la réaction de formation de chaque oxyde avec la convention ci-dessus, sans indiquer les états physiques des espèces intervenant.
- Compléter ce diagramme en indiquant pour chaque graphe le couple correspondant, sachant que l'aluminium est meilleur réducteur que le chrome.
- Aux points A, B et C, on observe un faible changement de pente. Préciser les transformations physiques qui expliquent ces changements de pente.
- Calculer à partir des données la valeur de la pente du segment DB puis celle du segment BC.
- On précise qu’à l’état solide ou liquide, les espèces Al, Al2O3, Cr et Cr2O3 sont totalement non miscibles. Ecrire l'équation de la réaction de réduction d’une mole de Cr2O3 par Al à 1300 K. Préciser s'il s'agit d'un équilibre chimique ou d'une réaction totale.

pression de 1,0 bar :
Corps pur
Température de fusion en K
Température d’ébullition en K
Aluminium Al
933
2740
Alumine Al2O3
2290
3250
Chrome Cr
2130
2940
Oxyde de chrome (III) Cr2O3
2710
4270
Données thermodynamiques :
H2(g)
O2(g)
H2O(g)
Al(s)
Al2O3(s)
Cr(s)
Cr2O3(s)
DfH° kJmol-1



-242


1676


-1140
S° JK-1mol-1
131
205
189
28
51
24
81
DfusH° kJmol-1




11
109
15


DvapH° kJmol-1




284


347


corrigé
Cr2O3 (s)+ 3H2 (g)= 2 Cr (s)+ 3H2O(g)

D H= 3 DfH° (H2O) - DfH° (Cr2O3) = -3* 242 +1140 = 414 kJ mol-1.

D S = 3 S° (H2O) + 2S°(Cr)- S° (Cr2O3)-3S°(H2)= 3*189 + 2*24-3*131-81 = 141 J K-1 mol-1.

D G= D H-T D S = 414000-1300*141 = 230700 J mol-1.

DG positif; donc réaction endothermique favorisée par une élévation de température.

ln K= - D G / ( RT) = -230700 / (8,31*1300) = -21,35

K= 5,3 10-10 donc réaction spontanée en sens inverse ( de droite à gauche).

4/3 Al + O2 = 2/3 Al2O3

4/3 Cr + O2 = 2/3 Cr2O3

Al , le plus réducteur, est situé en dessous de la droite CD

la droite du bas correspond à Al2O3 / Al.

A : fusion du chrome à 2130 K

B : fusion aluminium à 933 K

C : fusion alumine.

pente du segment DB : - DS de la réaction 4/3 Al + O2 = 2/3 Al2O3

D S = 2/3S( Al2O3 )- 4/3S( Al)-S(O2) = 2/3*51-4/3*28-205=34-37,3-205= -208,3 J K-1 mol-1

- DS = 208,3 J K-1 mol-1 .

pente du segment BC :

entropie de changement d'état à 933 K :

S= Dfusion H°(Al) / Tfusion = -11000 / 933= 11,8 J K-1 mol-1.

DS0= 2/3S0(Al2O3)- S0(O2)-4/3[S0(Al)+11,8]= 34-205-53 = -224 J K-1 mol-1.

- DS = 224 J K-1 mol-1 .

Cr2O3 (s)+ 2Al(l) = 2Cr (s)+ Al2O3(s)

D H = D (Al2O3)-DH ( Cr2O3) - 2Dfusion H°(Al)= -1676+1140-22 = -558 kJ mol-1

D S = S( Al2O3 ) + 2 S (Cr) - S( Cr2O3 )-2[ S( Al)+ Dfusion H°(Al) / Tfusion]

D S = 51+2*24-81-2(28 +11,8)= -61,6 J K-1 mol-1

D G= D H-T D S = -558000 + 61,6*1300 = -477900 J mol-1

ln K = 477900 / (8,31*1300) = 44.3

K= 1,7 10 24

K est très grand, donc réaction spontanée, totale dans le sens direct.


à suivre


retour - menu


à suivre