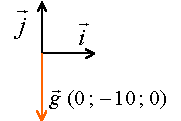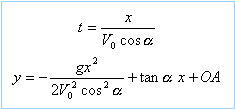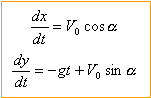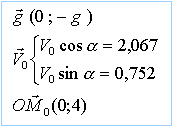| |
mouvement parabolique En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
|
le basketteur |
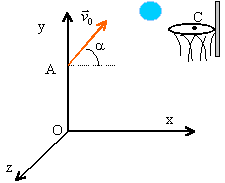
On négligera l'action de l'air. On prendra g = 10 m.s-2. Lors d'un match de basket, pour marquer un panier, il faut que le ballon passe dans un cercle métallique situé dans un plan horizontal, à 3,05 m du sol horizontal. Pour simplifier, on remplacera le ballon par un point matériel devant passer exactement au centre C du cercle métallique. xOy est un plan vertical contenant le point C ; xOz est le plan du sol supposé horizontal. D'un point A de Oy situé à 2,00 m du sol, un basketteur, sans adversaire, lance le ballon , avec une vitesse Vo contenue dans le plan xOy. Sa direction fait un angle a = 45° avec le plan horizontal. Vo = 9,2 m.s-1 masse du ballon = 700 g
corrigé |
|||||
| . . | |||||||
| |
V0cosa= 9,2 cos 45 = 6,5 ms-1. V0sina= 9,2 sin 45 = 6,5 ms-1. Système pseudo isolé : les actions mécaniques se neutralisent. Une fois lancé le ballon est soumis à son poids : il ne constitue pas un système pseudo isolé. vecteur accélération :
équation de la trajectoire :
coordonnées du vecteur vitesse à la date t :
seule la composante de la vitesse suivant la direction du poids est modifiée. Au sommet de la trajectoire , le vecteur vitesse est horizontal : la composante suivant Oy est nulle. D' où tS= V0sin a / g. Puis on remplace dans l'expression donnant l'ordonnée y. yS= 0,5 V0²sin²a / g + OA yS= 0,5*6,5² /10 + 2 = 4,11 m Au départ l'énergie est sous forme cinétique et sous forme potentielle de pesanteur (origine prise au sol) 0,5 mV0²+ mg OA 0,5*0,7*9,2² + 0,7*10*2 = 43,624 J En C l'énergie est sous forme cinétique et sous forme potentielle de pesanteur 0,5 mVC²+ mg OC = 43,624 VC²=(43,624 - 0,7*10*3,05) /0,35 = 63,64 -->VC=7,97 ms-1.
|
||||||
|
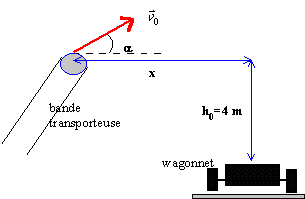
remblai dans un wagonnet |
|
||||||
| |
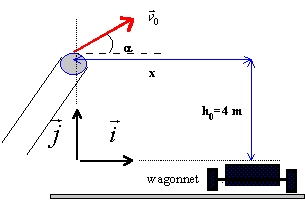
il faut préciser les coordonées du vecteur accélération, du vecteur vitesse initiale, du vecteur position initiale.
à la date t, le vecteur vitesse est une primitive du vecteur accélération: Vx = V0cosa = 2,067 Vy = -gt + V0sina =-9,8 t + 0,752 à la date t, le vecteur position est une primitive du vecteur vitesse: x = V0cosa t = 2,067 t y = -0,5gt² + V0sina t + 4 = -4,9 t² + 0,752 t + 4 Eliminer le temps entre ces 2 relations pour obtenir la trajectoire . y = -1,147 x² + 0,364 x +4 calcul de la distance x, ou portée : écrire que y = 0, puis résoudre l'équation du second degré . On trouve : 2,03 m hauteur maximale atteinte : écrire que le vecteur vitesse est horizontal (composante verticale nulle) d'où t = 0,752 / 9,8 = 0,0767 s remplacer t par cette valeur dans y : yS= -4,9 *0,0767² + 0,752 *0,0767 + 4 yS= 4,029 m
|
||||||
|
|
|
||||||