| |
le grand looping Inde 04 /98 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||||||||||||||
|
|
mouvement circulaire non uniforme action du support |
On étudie le mouvement du centre d'inertie G d'un chariot de fête foraine. Le chariot dispose d'un double jeu de roulettes: un premier sur les rails et un second dessous pour empécher la perte de contact quelle que soit la situation. On considérera le chariot comme une masse ponctuelle réduite au centre d'inertie G. On distingue 4 parties dans la trajectoire de G: 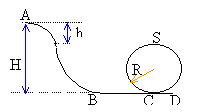 la partie AB ou rampe de lancement : altitude de A =12m au dessus de B la partie BC rectiligne horizontale la partie CSC constitue le looping rayon du cercle R= 3,8 m dans un plan vertical la partie CD représente la sortie du looping vitesse initiale en A nulle masse du chariot : m = 200 kg. les frottements sont négligés rampe de lancement AB:
mouvement horizontal BC:
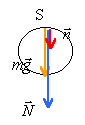
sommet du looping:
|
|||||||||||||||||
| |
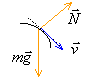
le poids effectue un travail : mgh l'action du plan perpendiculaire à la vitesse ne travaille pas th de l'énergie cinétique entre A et un point M quelconque du parcours AB: ½ mv²M- 0 = mgh d'où v²M = 2gh.
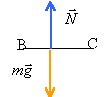
Les deux forces sont opposées: le mouvement est rectiligne uniforme entre B et C avec la vitesse aquise au passage en B soit v²B= 2gH et vB= 15,3 m/s
le poids et l'action du support sont des forces de direction verticale; le poids est dirigé vers le bas. la somme de ces deux forces est un vecteur de direction verticale; l'accélération est donc un vecteur de direction verticale. l'accélération est toujours dirigée vers l'intérieur de la trajectoire : donc l'accélération est orientée vers le bas, passant par le centre du cercle. La valeur de l'accélération normale est : v²S/ rayon = 9,3² / 3,8 = 22,76 m/s² soit 2,3 fois plus grande que la valeur de g Le théorème du centre d'inertie projeté sur l'axe n de la base de Frenet s'écrit : N + mg = m aS = v²S / R N= mv²S / R -mg = 200*( 22,76-9,81) = 2590 N
|
||||||||||||||||||
|
|
|