| |
circuit RL Amérique du Sud 12 /98 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
|
inductance constante de temps |
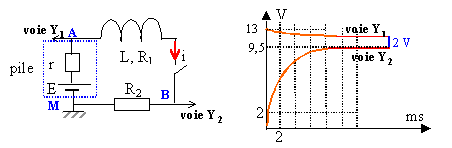
R2 = 50 W. Un ordinateur relié au montage par un interface approprié permet d'enregistrer les tensions au cours du temps.
|
|||||
| |
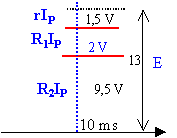
Les phénomènes d'induction ne se manifestent que lorsqu'il y a une variation de champ magnétique ou une variation de l'intensité du courant dans ce cas. Ils n'existent que pendant cette variation. En régime permanent le phénomène d'induction n'existe plus et la bobine garde en réserve l'énergie ½ LIP². voie (1) , on observe la tension UAM et voie (2) la tension UBM aux bornes d'un résistor, donc l'image de l'intensité. A l'instant t = 0, l'intensité est nulle et la fem de la pile est égale à 13 V.
en régime permanent le terme L di/dt est nul UAM = E- r IP ; UAB = R1IP ; UBM = R2IP ; UAM =UAB + UBM
50 IP = 9,5 d'où Ip = 0,19 A R1 = 2 / 0,19 = 10,5 W. r = 1,5 / 0,19 =7,9 W. inductance : henry ; or U (volt) = L (henry) di/dt ( ampère / seconde) soit L homogène à : [V] [A]-1 [s]. R homogène à : [V] [A]-1 d'où L / R homogène à un temps R représente la résistance totale du circuit : 50+10,5+7,9 = 68 ,4 W. lorsque le temps devient suffisamment grand devant la constante de temps ( environ 5 fois plus ) l'exponentielle tend vers zéro ; on atteint le régime permanent : donc A = IP. le régime permanent est atteint au bout de 5 t soit environ 9 ms t voisin de : 1,8 10-3 s. 1,8 10-3 = L / 68,4 d'où L = 0,12 H. énergie stockée en régime permanent : ½ LIP² = 0,5*0,12*0,19² = 2,1 mJ
|
||||||
|
|
|