| |
Jupiter, les Grecs, les Troyens sujet complémentaire En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
|
satellites base de Frenet |
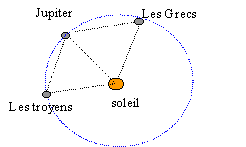
On a observé dans l'orbite de Jupiter deux amas de petites planètes, surnommées les Grecs et les Troyens.. Soit un système isolé de 2 corps ponctuels identiques, de masse M en interaction gravitationnelle. Ces deux corps ayant initialement ( dans un référentiel lié à O) les vecteurs vitesses représentés sur la figure. On constate que leur mouvement ultérieur sont circulaires uniformes, à la vitesse angulaire W0. 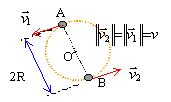
|
|||||
| |
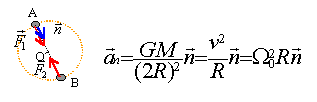
les corps A et B exercent entre eux des forces de gravitation, attractives, proportionnelles aux masses et inversement proportionnelles au carré de la distance ( d=2R) qui les sépare. O est le centre d'inertie des corps A et B de masse égale à M. Le référentiel d'étude est lié à O. Ecrire la deuxième loi de Newton suivant l'axe n de la base de Frenet l'accélération normale est égale à la vitesse au carrée divisé par le rayon du cercle. Or vitesse linéaire et vitesse angulaire sont liées par la relation v=W0 R. d'où W0=(GM / (4R3) ½. 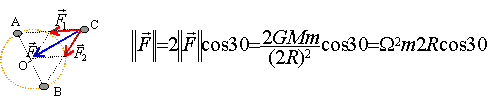
le corps C de masse m <<M ne modifie pas la position du centre d'inertie O des corps A et B. Le référentiel d'étude est lié à O. Faire la somme vectorielle des forces F1 et F2, force de gravitation de même norme norme de F1 = GMm / (2R)² La force F est dirigée vers le centre du cercle O: en conséquence l'accélération tangentielle est nulle et le mouvement du corps C est circulaire et uniforme. l'accélération normale est 2GM cos 30 / (2R)² = v² / (2R cos30) = W² 2R cos 30. d'où W²= GM / (4R3)= W²0. Le point cherché possédant les propriétés de C est le symétrique de C par rapport à O. La masse du soleil étant 1000 fois plus grande que celle de Jupiter, le centre d'inertie du système Soleil Jupiter est pratiquement confondu avec le soleil. Le soleil est donc le référentiel.
|
||||||
| |
|