Aurélie avril 2001


devoirs en terminale S

interférences bac juin 98

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


1

interfrange, trou d'Young, analyse dimensionnelle

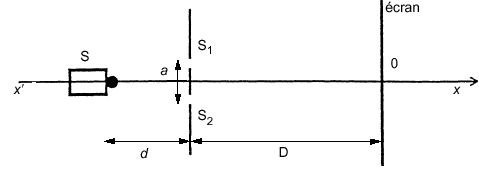
Le dispositif comprend une plaque percée de deux trous de Young distants de a =500 µ m. En utilisant comme source émettrice S un laser He-Ne, de longueur d’onde l= 633 nm on produit des interférences sur un écran. La plaque est placée à une distance d =20 cm de la source, l’écran à une distance D = 4 mde la plaque. Les deux trous de même diamètre sont placés à égale distance de la source et se comportent comme deux sources synchrones et cohérentes.

  2. Expliquer le phénomène d’interférences en quelques lignes.
  3. Au point O, la frange est-elle brillante ou sombre ? Justifier.
  4. Les franges brillantes sont équidistantes. L’intervalle qui les sépare est appelé interfrange et noté i . On cherche à connaître les paramètres dont peut dépendre i (nature de S, a , d , D) et à en donner une expression parmi les propositions suivantes :
  5. Par l’analyse dimensionnelle, éliminer une ou plusieurs propositions.
  6. En réalisant plusieurs expériences, où l’on fait varier un seul paramètre en laisant les autres identiques, on effectue les constatations suivantes :

    -L’utilisation d’un laser vert montre que l’interfrange diminue ;

    -Si on éloigne l’écran, l’interfrange augmente ;

    - La position de S sur l’axe ne modifie pas l’interfrange ;

    - Les deux trous étant rapprochés de l’axe , les franges s’écartent les unes des autres.

    En utilisant ces résultats, trouver parmi les propositions (a), (b), (c), (d), (e), l’expression de l’interfrange i , en justifiant le raisonnement.

    Donner la valeur de l’interfrange i obtenue avec le laser He-Ne.

...

corrigé



On observe un phénomène d ’interférences lumineuses en tout point d ’un

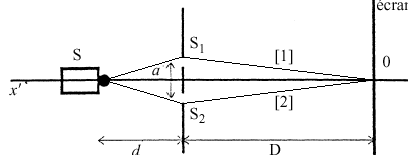
écran où se superposent les 2 faisceaux lumineux issus des 2 sources secondaires S1 et S2.

Ces 2 faisceaux lumineux issus d ’une même source ponctuelle S sont cohérents.

interférences constructives et sur l ’écran, on a une raie brillante.

Si les 2 vibrations qui interfèrent sont en phase, l’amplitude de la vibration est maximale.

interférences destructives et sur l ’écran, on a une raie sombre.

Si les 2 vibrations qui interfèrent sont en opposition de phase, l’amplitude de la vibration est nulle.

Pour atteindre le point O, les vibrations lumineuses parcourent la même distance qu'elle prenne le chemin [1 ] ou le chemin [2 ]. La différence de marche est nulle.

Les 2 vibrations qui interfèrent en O sont alors en phase :

frange brillante et interférences constructives.

analyse dimensionnelle :

l, D, a, d et i sont des longueurs :[L]

(a) lD/a expression possible car [L] [L] [L]-1 = [L]

(b) lD² expression impossible car [L] [L] [L] = [L]3

(c) Da / l expression possible car [L] [L] [L]-1 = [L]

(d) la/D expression possible car [L] [L] [L]-1 = [L]

(e) ld/a expression possible car [L] [L] [L]-1 = [L]

recherche de la bonne expression de l'interfrange :

lvert < lrouge et l'interfrange i diminue: i et l varie donc dans le même sens.

(c) Da / l éliminé.

D augmente, alors l'interfrange i augmente: D et i varie dans le même sens.

(d) la/D éliminé

la position de S sur l'axe xx' ne modifie pas l'interfrange: i indépendant de d

(e) ld/a éliminé

la distance S1S2 = a et l'interfrange i varie en sens contraire

(a) lD/a expression correcte.

calcul de l'interfrange :

l = 633 nm = 6,33 10-7 m

D= 4 m; a = 5 10-4 m

i = 6,33 10-7 *4 /5 10-4 = 5,06 mm.


à suivre ...
retour - menu
à bientôt ...