| |
étude de la résonance d'intensité d'un circuit RLC série France bac 06 /98 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|||||||||||||||||||
|
|
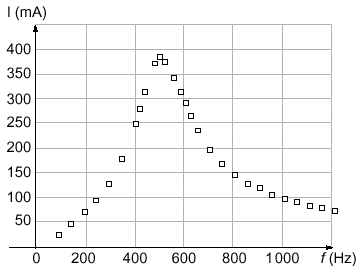
facteurs influençant la résonance
|
Un circuit comprend, montés en série, un conducteur ohmique de résistance R=10 ohms, une bobine d’inductance L = 10mH et de résistance r =2,5 ohms, un condensateur de capacité C= 10 mF, un générateur basse fréquence (GBF) délivrant une tension sinusoïdale, réglable en fréquence, et de valeur efficace constante U=5 V . 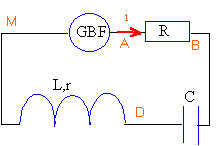 Étude de la résonance
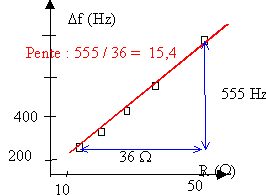
influence de la résistance sur la bande passante D’autres séries de mesures réalisées en modifiant seulement la valeur de la résistance totale du circuit conduisent aux résulats ci-dessous :
|
||||||||||||||||||
| |
Pour visualiser la tension uMA aux bornes du GBF, le point M est relié à la voie 1 de l'oscilloscope et le point A est relié à la masse. Pour visualiser la tension uBA aux bornes du résistor, le point B est relié à la voie 2 de l'oscilloscope et le point A est relié à la masse. Aux bornes d'un résistor, intensité et tension sont proportionnelles : l'image de la tension aux bornes de ce résistor est l'image de l'intensité au facteur R près.
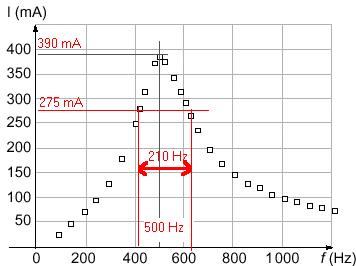
valeur maximale de l'intensité efficace : à la résonance l'impédance du circuit RLC est minimale, égale à la résistance totale du circuit Imaxi = 5 / (10+2,5) = 0,4 A lecture graphe 0,39 A. bande passante : ensemble des fréquences telles que l'intensité efficace soit supérieure à :390 / 1,414 = 275 mA . On lit Df voisin 210 Hz. fréquence propre de l'oscillateur LC : 1 /(2p racine carrée (LC)) = 1 /(6,28 racine carrée (0,01*10-5 ))= 503 ,5 Hz.
La bande passante et la résistance du circuit sont proportionnelles. 15,4 = 1 / (2p L) où L = 1 /(6,28*15,4 ) =0,0103 H.
dimension de R / (2pL) : 2p est sans dimension R : [V] [A]-1. L : [H] = [V] [s] [A]-1. remarque u=Ldi / dt. R / L : [s]-1. Df : [Hz]=[s]-1.
|
|||||||||||||||||||
|
|
|