Aurélie janvier 2001


devoirs en terminale S

dipole RL Amérique du sud bac 12 / 98

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


1

circuit RL

constante de temps

inductance

 

 

  On branche en série une pile de fem E et de résistance interne r, un interrupteur K, une bobine inductive d'inductance L et de résistance R1, et un résistor R2.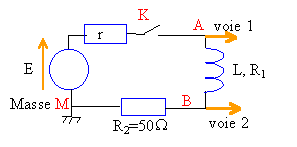

Un ordinateur relié au montage par une interface appropriée, permet d'enregistrer au cours du temps les valeurs des tensions.

  1. A l'instant t=0, on ferme l'interupteur K et on procède à l'enregistrement. On obtient les courbe y1(t) et y2(t) ci-dessous. Quelles sont les grandeurs électriques observées sur les voies 1 et 2 . Identifier y1 et y2. Justifier.

  2. A partir de la courbe représentant la variation de l'intensité dans le circuit, expliquer le comportement électrique de la bobine. Donner la valeur de la force électromotrice E de la pile.
  3. Lorsque le régime permanent est établi, l'intensité prend la valeur I tandis que y2 prend la valeur Y. Donner les expressions littérales des tensions uAM, uAB, uBM. Montrer en utilisant les courbes que la bobine a une résistance électrique R1 non nulle.
  4. Calculer I, la résistance interne r de la pile, la résistance R1 de la bobine.
  5. Le circuit étudié peut être caractérisé par une constante de temps t qui permet d'évaluer la durée nécessaire à l'établissement d'un régime permanent . Pour un circuit RL on pose t =L / R
  • Montrer que t est homogène a un temps.
  • Que représente R dans le circuit étudié ? Quelle est sa valeur numérique ?.
  • On admet que l'intensité dans le circuit est de la forme i(t) = A(1-exp (- t/ t )). Montrer que A est égal à I.
  • Donner la valeur de t déterminé graphiquement.
  • En déduire la valeur de L
  • Calculer l'énergie emmagasinée par la bobine quand le régime permanent s'établi.

     

.
.

corrigé



La tension aux bornes de la pile n'est jamais nulle (sauf pile usée).

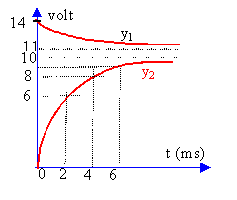
Sur la voie 1 on visualise uAM, tension aux bornes de la pile, générateur de tension imparfait.

y1 correspond à uAM.

A l'instant où l'on ferme le circuit, l'intensité est nulle et la tension aux bornes de la pile est égale à sa fem soit E=14 V (lecture graphe y1).

Sur la voie 2 on visualise la tension uBM, aux bornes d'un résistor.

A l'instant où l'on ferme le circuit, l'intensité est nulle et la tension aux bornes du résistor R2 est nulle.

y2 correspond à uBM.

La bobine stocke de l'énergie lors de la fermeture de l'interrupteur ce qui a pour conséquence de retarder l'établissement d'un régime permanent (intensité constante dans ce cas).

en régime permanent :

Y = 9,5 V lecture graphe y2.

9,5 = 50 I d'où I = 0,19 A.

uBM = 50 I =Y =9,5 V

La bobine se comporte comme une résistance uAB = R1 I = 0,19 R1.

si R1 voisin de zéro alors uAM voisin de uBM.

Or la lecture des graphes pour un temps supérieur à 10 ms montre une différence entre uAM et uBM.

Cette différence représente uAB tension aux bornes de la bobine en régime permanent.

uAB voisin de 2V (lecture graphe) d'où R1 voisin de 2 /0,19 = 10,5 W.

uAM = E-rI =14-0,19 r voisin de 11,5 V (lecture graphe à t supérieur à 10 ms)

0,19 r = 2,5 d'où r = 13,1 W.

équation aux dimensions

L : [H] = [V] [A] -1 [s]. remarque u=Ldi / dt aux bornes bobine pure.

R :[W]= [V] [A]-1.

L / R : [V] [A] -1 [s] [A] [V]-1 = [s]

R représente la somme de toutes les résistances du circuit soit R = r +R1 + R2 = 73,6 W.

intensité

Lorsque le temps devient grand (supérieur à 5 fois la constante de temps) l'exponentielle tend vers zéro et A représente l'intensité en régime permanent soit I=0,19 A.

constante de temps détermination graphique y2.

L'intensité est constante à partir d'une durée voisine de 5t soit environ 10ms d'où t voisin 2 ms.

La valeur de l'intensité est égale à 0,63 I à un temps égal à t.

soit uBM voisin de 0,63*9,5 = 6V d'où t voisin 2 ms.

le coefficient directeur de la tangente à la courbe y2 à t=0 est égal à R2I / t = 9,5 / t.

inductance et énergie stockée :

L = R t =73,6* 2 10-3 = 0,15 H.

énergie : 0,5 L I² = 0,5 *0,15*0,19² = 2,7 mJ.


à suivre ...
retour - menu
à bientôt ...