| |
tension aux bornes d'un condensateur, intensité dans une bobine . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
calcul de la capacité et de l'inductance
|
On considère un générateur basse-fréquence qui délivre une tension de forme "créneau", dont l'am-plitude E et la fréquence f sont constantes, mais réglables par l'expérimentateur. On réalise deux séries d'expériences au cours desquelles ce générateur alimente successivement les deux circuits suivants : 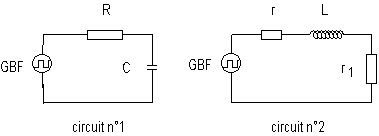
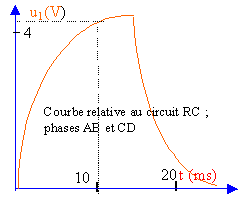
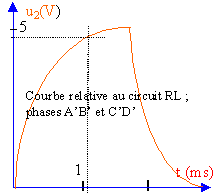
Le circuit n°1 comporte un condensateur de capacité C en série avec une résistance R ; le circuit n°2, une bobine de résistance r et d'inductance L en série avec une résistance r1 . On observe, à l'aide d'un oscilloscope, les tensions u1(t), aux bornes du condensateur, et u2(t), aux bornes de la résistance r1. La période T de la tension délivrée par le générateur est choisie assez grande de façon qu'à la fin de chaque demi-période, ces deux tensions soient pratiquement constan-tes. La vitesse de balayage est choisie de façon à pouvoir observer au moins une période. Soit T1, la valeur de T choisie pour le circuit n°1 et T2 , celle choisie pour le n°2. L'oscilloscope utilisé est relié à un ordinateur muni d'une carte d'acquisition de données. On dispose alors dans des tableaux numériques des valeurs des tensions acquises à intervalles de temps régu-liers. Les courbes ci-dessous donnent, pour une durée égale à T, les oscillogrammes relatifs aux deux circuits.
Données théoriques : - Cas du circuit RC On définit une constante de temps : t1 = RC . L'expression de la tension aux bornes du condensateur est différente suivant la phase considérée. Pendant la première demi-période , phase AB, on a la forme : u1 (t) =U(1-exp(-t/t1)) (1) Pendant la deuxième demi-période , phase CD, on la forme : u2(t) = U(exp(-t/t1) (2) une nouvelle origine des temps a été prise : t' = 0 pour t = T1 /2. - Cas du circuit RL Soit Ro = r + r1, la résistance totale du circuit ; on définit une constante de temps : t2 = L/Ro. L'ex-pression de la tension aux bornes de la résistance r1 est différente suivant la phase considérée. Pendant la première demi-période , phase A'B', on a la forme : u'1(t) =U1(1-exp(-t/t2)) (3) Pendant la deuxième demi-période , phase C'D', on a la forme : u'2(t) = U1exp(-t/t2) (4) avec la même remarque qu'en (2) pour la nouvelle origine des temps.
1. Détermination rapide de t à partir des graphiques: On dit très souvent qu'un condensateur chargé sous une tension constante a atteint 95 % de sa ten-sion maximum "au bout d'un temps égal à 3t".
2. Vérification des relations théoriques Le système d'acquisition de l'ordinateur permet d'obtenir les tableaux de valeurs correspondant à deux expériences relatives à chacun des circuits. Des extraits de ces tableaux concernant les phases CD et C'D' sont donnés ci dessous.
u(t) = f(t); u(t) = f[ln(t)] ; ln[u(t)] = f(t) Justifier brièvement le choix qui a été fait. [Remarque : u et t représentent les valeurs numériques de la tension u et du temps t dans les mesures proposées ; ils sont donc sans dimensions].
3. Détermination plus précise des constantes de temps Le logiciel de calcul de l'ordinateur donne également une vérification excellente des relations (1) à (4). En particulier, il propose, compte tenu des points qui ont été acquis, les modèles mathématiques suivant : - phase AB, pour la tension u1(t), le modèle Umod u1 mod=K1(1-exp at) avec K1= 4,193 et a = -373,4 si Umod est exprimée en volts et t en secondes. - phase A'B', pour la tension u2(t), le modèle Vmod
|
||||||||||||||||||||||||||||||||||||||||||||||
| |
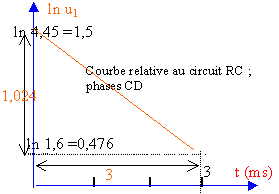
le second graphique représente la tension aux bornes d'un résistor. Aux bornes d'un résistor, tension et intensité sont proportionnelles. u2(t) est l'image de l'intensité du courant. La présence de la bobine inductive provoque un retard à l'établissement du courant. t2 donne une idée de ce retard. lecture graphique : 3 t2 voisin de 1 ms soit t2 voisin de 0,33 ms. les tensions u1 et u2 ne sont pas proportionnelles au temps : u=f(t) n'est pas à retenir, les courbes obtenues seraient des exponentielles décroissantes. à partir des expressions (2) ou (4) remarquons que : ln u = ln U - t / t. y correspond à ln u ; x correspond au temps (ms); b= ln U=ln4,45 =1,5 et a =-1 /t1 avec t1en ms c'est à dire qu'en traçant ln u en fonction du temps on obtient une droite d'ordonnée à l'origine ln U et de pente -1 / t.
coefficient directeur : -1,024 /3 = -1 / t1.D'où t1=2,93 ms même travail pour déterminer t2 : (ln5 ,2- ln 0,18 ) / 0,9 =3,73 et t2 =0,267 s. K1 et K2 sont des tensions en volt a et b correspondent à l'inverse d'un temps ou encore à l'inverse des constantes de temps t1 et t2. application numérique : t1 = 1 / 373,4 = 2,67 10-3 s =2,67 ms. 2,67 10-3 = RC = 58,2 103 C C= 45,87 10-9 F = 45,87 nF. t2 = 1 / 4183 = 2,39 10-4 s = 0,239 ms. 2,39 10-4 = L / 209 L= 50 mH.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|