Aurélie janvier 2001


devoirs en terminale S

mouvement rectiligne uniformément varié

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

 


1

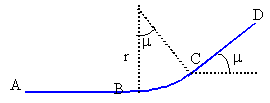
voiture en panne

Une automobile en panne de moteur, assimilable à un solide en translation, a une masse M=1200 kg. Elle est poussée par un véhicule de secours. Le démarrage de l'automobile en panne sur une route rectiligne et horizontale commence par une phase d'accélération pendant laquelle le véhicule qui la pousse exerce une force constante F parallèle au déplacement et dirigée vers l'avant. Dans cette question, on admettra qu'aucune force ne s'oppose à l'avancement de l'automobile. On se propose d'étudier le mouvement du centre d'inertie G de l'automobile. A la date t=0, instant du démarrage, G se trouve à l'origine de l'axe O avec une vitesse nulle.

  1. Effectuer le bilan des forces extérieures agissant sur l'automobile.
  2. L'automobile atteint la vitesse v=120 km/h après un parcours de 600 m. Etablir l'expression de l'accélération en fonction des données du texte. En déduire les expressions de la vitesse et de l'abscisse x en fonction du temps.
  3. Etablir, à partir de ces expressions, celle reliant v(x)carré, a(x) et x. Calculer a(x). En déduire la valeur de F.
  4. Suite au parcours précédemment effectué à la suite duquel la voiture avait atteint la vitesse de 120 km/h, celle-ci est libérée de l'action de poussée au point A. Elle arrive alors sur cette portion de route.

    AB rectiligne parfaitement horizontale de longueur L1.
    BC circulaire de centre O de rayon r = 100 m. OC fait un angle µ = 15° avec la verticale.
    CD rectiligne de longueur L2 faisant un angle µ = 15° avec l'horizontale.
    Dans toute cette partie, les frottements sont négligés, sauf sur la partie CD pour laquelle ils équivalent à une force f de valeur constante. L'automobile arrive en B. Justifier, sans calculs, que v(b)=120 km/h.

  5. En appliquant le théorème de l'énergie cinétique au véhicule, sur le tronçon BC, établir l'expression de v(c) en fonction de v(b), r, g et µ.
  6. Calculer numériquement v(c). On prendra g = 9,81 N/kg.
  7. L'automobile s'arrète sur le tronçon CD après avoir parcouru une distance de 150 m. En utilisant le théorème de l'énergie cinétique, calculer la valeur de la force de frottements s'exerçant sur CD.
corrigé
.
.

poids opposé à l'action du support

force motrice parallèle au plan horizontal

la relation fondamentale de la dynamique s'écrit alors : F = Ma

120km/h=120/3,6 =33,33 m/s

v²-vo²=2a distance (1) avec vo, vitesse initiale nulle

33,332=2*600*a

a=0,925 m/s²

vitesse, primitive de l'accélération : v = 0,925 t

position, primitive de la vitesse : x =0,925 / 2 t² = 0,46 t²

éliminer le tempspour retrouver (1)

F = Ma =1200*0,925=1110 N

 

ou bien th de l'énergie cinétique, seule F travaille

0,5 M v²=F distance = Ma *distance

 

entre A et B voiture pseudo isolée, aucune force ne travaille donc pas de

modification de la vitesse.

entre B et C seul le poids travaille: -mgr(1-cos m) (action du plan

perpendiculaire au plan)

0,5 mv²c-0,5 mv²b= -mgr(1-cos m)

v²c=  v²b-2gr(1-cos m)

v²c=33,33 2 -2*9,8*100(1-cos15) =1144

vc=32,31 m s-1.


entre C et D

travail du poids : -mg CD sin m

travail des frottements : -f CD

variation d'énergie cinétique : -0,5 mvc²

th de l'énergie cinétique :

-0,5 mvc² = -mg CD sin m -f CD

f = m(0,5 vc² / CD -g sin m)

f = 1200(0,5*32,312/150 -9,8 sin15)

f = 1140 N 

2

palet sur plan incliné
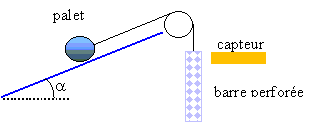Pour étudier le mouvement d'un palet autoporté sur un plan incliné, une barre métallique percée de fentes équidistantes est fixée au palet par l'intermédiaire d'un fil inextensible.

Données: accélération de la pesanteur: g = 9,81 m.s-2. Masse du palet: m = 712 g. Masse de la barre: m' = 34 g. Pour toute l'expérience, les approximations suivantes sont admises:

-la masse de la barre perforée est négligeable devant celle du palet;

-la poulie, de masse négligeable, tourne sans frottements autour de son axe.

  1. Le déplacement, vertical vers le haut, de la barre perforée permet grâce au capteur de tracé le graphe de la variation de la vitesse v en fonction du temps. Le coefficient de la droite obtenue est égal à 1,725. Quelle est la signification physique de ce coefficient directeur, pour le mouvement de la barre perforée? En déduire la nature du mouvement de la barre perforée.
  2. En considérant la barre perforée, déterminer les caractéristiques de la tension T du fil accroché à la barre. Dans la suite du problème, on admettra que la valeur de cette tension se conserve le long du fil.
  3. Comparer le mouvement du palet autoporté à celui de la barre perforée. En déduire la nature du mouvement du palet. Etablir une expression littérale de l'accélération du mouvement du palet.
  4. Calculer la valeur de l'angle a entre le plan incliné et l'horizontale.
corrigé


vitesse= accélération fois temps+ vitesse initiale

1,725 m/s² accélération

mouvement rectiligne uniformément accéléré

La barre perforée est soumise à deux forces verticales de sens contraire, le poids de la barre et la tension du fil. La 2ème loi de Newton s'écrit en projection sur un axe vertical ascendant :

tension -m'g =m'a

T=m'(a+g)=0,034*(1,725+9,8)= 0,39 N

palet :

la masse de la poulie étant négligée, l'accélération du palet est identique à celle de la barre perforée. Le palet est soumis à 3 forces, l'action du plan normale au plan, son poids vertical vers le bas et la tension du fil, parallèle au plan.

projection de la somme vectorielle des forces sur un axe parallèle au plan dirigé vers le bas

mgsin a -tension = ma

a est constante si T est constante

donc mouvement du palet rectiligne uniformèment accéléré

sin a =(tension / m + a) / g= (0,39/0,712 +1,725)/9,8 =0,232

a = 13°

 

3

toboggan

Un enfant de masse m , se laisse glisser sur un toboggan constitué d'un plan incliné de longueur Let faisant un angle alpha avec l'horizontale.Ce plan est suivie d'une partie horizontale.

L' enfant subit une force de frottement de valeur cste sur tout le trajet.Il se lance du haut du toboggan avec une vitesse Vo et il s' immobilise spontanément sur la partie horizontale du toboggan apès avoir parcouru une distance d .

  1. Faire le bilan des forces appliqués à l'enfant pr les 2 parties de la trajectoire (les représentés sur un shéma).
  2. Donner l' expression littérale de la force de frottement
corrigé


 

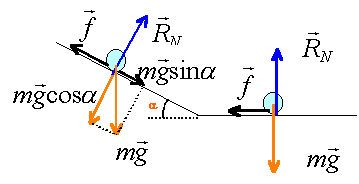
sur le plan incliné :

-f + mgsina=m a1

et v²-v0²= 2 a1 L avec v : vitesse en bas du plan

a1 = -f / m +gsina

donc v²-v0²= 2 L( -f / m +gsin a ) (1)

 

sur la partie plane :

-f = ma2

et 0-v²=2 a2 distance

v²=2f / m distance

repport dans (1)

2f distance / m -v0² = 2 L ( -f / m +gsin a )

 

ou bien théoréme de l'énergie cinétique entre le point de départ et l'arrêt

travail des frottement : -f(d+L)

travail du poids lors de la descente : mgLsina

variation énergie cinétique : -0,5 mv0²

-0,5 mv0²=-f(d+L)+mgLsina



à suivre ...
retour - menu
à bientôt ...