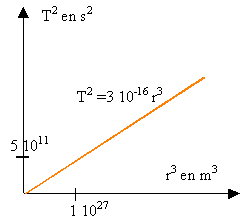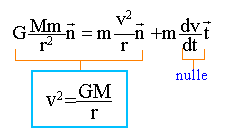| |
éphémérides ( France bac septembre 2000) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
|
exploitation des courbes |
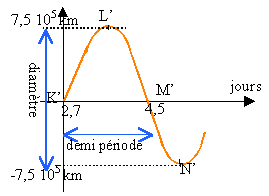
Autour de la planète Jupiter gravitent des satellites naturels. Les quatre plus gros sont Io, Europe, Ganymède et Callisto. Dans un référentiel centré sur Jupiter supposé galiléen, on considère que le centre de chacun des satellites est animé d'un mouvement circulaire uniforme autour du centre J de Jupiter. Sur la figure 1 (ci-dessous), on a représenté uniquement la trajectoire du centre d’inertie E d'Europe. Les trajectoires des autres satellites appartiennent sensiblement à ce même plan qui contient aussi le centre T de la Terre. 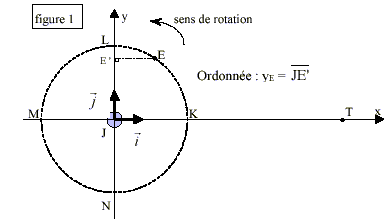 Une revue d'astronomie a publié les courbes donnant les variations, en fonction du temps, de l'ordonnée y de chacun des quatre satellites dans le repère orthonormé . (voit figure 1). Les courbes ou éphémérides obtenues entre le 21 avril 1997 à 00 h 00 et le 2 mai 1997 sont données en annexe 1 à rendre avec la copie. Pendant la durée de l’observation, la Terre sera considérée comme immobile par rapport au référentiel choisi. La distance TJ est très grande devant le rayon des trajectoires des satellites. La figure n'est pas à l'échelle. 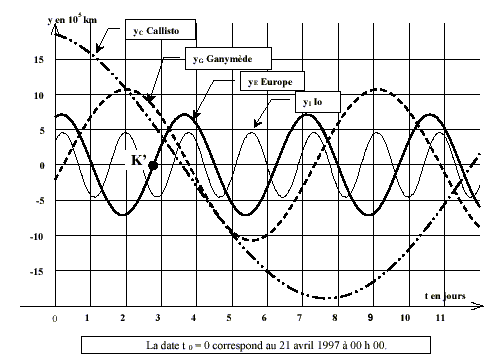
|
|||||
| |
le couple ( K' M' )permet de déterminer la demi période soit environ 1,8 jours. période voisine de 3,6 joursle couple ( L' N' )permet de déterminer le diamètre soit environ 1,5 106 km. Io est le plus proche de Jupiter; Callisto est celui qui a la plus grande période.
|
||||||
|
déterminer la masse de Jupiter |
On considère que chaque satellite de masse m n’est soumis qu’à la seule force gravitationnelle de la part de Jupiter de masse M et que les astres ont une répartition de masse à symétrie sphérique. On note r le rayon de la trajectoire circulaire décrite par les satellites autour de Jupiter. r représente la distance entre le centre de Jupiter et le centre du satellite étudié.
a. En observant ce graphe, pourquoi peut-on dire que la troisième loi de Kepler est vérifiée ? b. L’équation de la meilleure droite passant par les points obtenus est :T 2 = 3 × 10 -16 r 3 . En déduire l’ordre de grandeur de la masse de Jupiter. On prend p ² = 10 et G = 1 ×10 -10 unité SI. corrigé |
||||||
| |
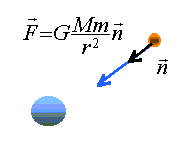
la dérivée de la norme du vecteur vitesse par rapport au temps étant nulle, alors la norme de la vitesse est constante et le mouvement est uniforme. La vitesse du satellite est indépendante de sa masse, est d'autant plus grande que le rayon de l'orbite est petite.( le plus proche de Jupiter) . période : durée pour décrire la circonférence à la vitesse v, norme constante. 2pr = vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² r² =GM / r T² ou T² =4p² /(GM) r3. ( 3 ème loi de Kepler) Le graphe proposé est une droite, donc le carré de la période est proportionnel au cube de la distance des centres. 3 10-16 = 4p² /(GM) M= 4*10 /(10-10*3 10-16)=1,33 1027 kg
|
||||||
|
|
|