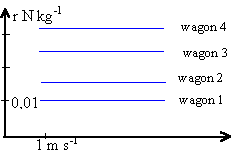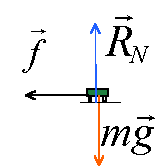| |
gare de triage ( France bac juin 98) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
|
étude du coefficient de résistance à l'avancement r |
Dans tout l'exercice, les wagons seront assimilés à des solides en translation, leurs mouvements seront étudiés dans le référentiel terrestre supposé galiléen. Les résistances aux passages dans les courbes et les perturbations liées aux changements de pente seront négligées. Dans une gare de triage, les wagons sont séparés au sommet d'une butte ( Ils descendent un à un la rampe R et ils sont ensuite aiguillés vers une voie de garage où ils devront arriver au contact d'autres wagons pour former un nouveau train. Cette opération, appelée le "tir au but" par les professionnels, utilise des freins de voie F1 et F2. 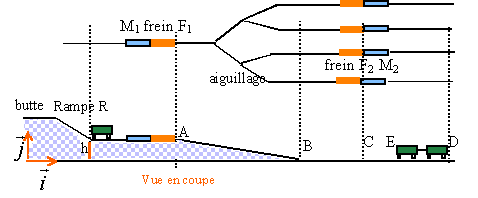 On appelle base de mesure M un dispositif comportant différents types de capteurs. La base de mesure M1 est utilisée pour la détermination du coefficient de résistance r à l'avancement et la base de mesure M2 est un autre dispositif utilisé pour la détermination de la longueur de rail restant à parcourir. L'ensemble de ces dispositifs permet la régulation de la vitesse de chaque wagon. Les frottements qui s'exercent sur un wagon sont modélisés par une force et de valeur f = m.r, opposée au déplacement , où m est la masse du wagon et r le coefficient de résistance à l'avancement.
|
|||||
| |
r = f(v) est une fonction constante. r voisin de 0,033 N kg-1 (wagon 4).
la somme vectorielle des forces appliquées au wagon est égale au produit de la masse par l'accélération. Suivant l'axe j : RN = mg et suivant i : -f = ma avec f= m r d'où la norme de l'accélération est égale à r. le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps : v=-k t +p donne v' = a = -k avec en plus norme de l'accélération = r.
|
||||||
|
rôle du frein primaire |
Situé derrière la base de mesure M1, ce frein doit laisser à chaque wagon une vitesse de valeur vA suffisante, à sa sortie en A, pour qu'il puisse atteindre l'extrémité D des voies de garage avec une vitesse de valeur vD. On ne tiendra pas compte dans cette partie du frein secondaire.
corrigé |
||||||
| |
travail des frottements : - f AB = -mrAB travail du poids : mgh l'action RN normale au plan ne travaille pas. sur le trajet BD: travail des frottements : - f BD = -mrBD le poids, perpendiculaire au plan, ne travaille pas l'action RN normale au plan ne travaille pas. au total : mgh - mr(AB+BD)= m(gh-rL) La somme des travaux ci dessus est égale à la variation de l'énergie cinétique : 0,5 mv²D-0,5 mv²A =m(gh-rL) v²D-v²A = 2(gh-rL) v²A = 2(rL-gh) +v²D. calcul de la vitesse en A, la vitesse en D étant nulle : v²A = 2(0,032*800-9,8*1) = 31,6 et vA=5,62 ms-1.
|
||||||
|
rôle du frein secondaire |
En réalité, on souhaite amener le wagon au contact des wagons déjà présents sur la voie de garage et obtenir son accrochage automatique. Du fait du remplissage des voies de garage, la distance qui reste à parcourir est variable suivant le nombre de wagons déjà présents. La position du dernier wagon sur la voie sera fournie par la base de mesure M2. Le frein secondaire va prendre en compte ces autres paramètres pour réaliser le tir au but avec précision.
corrigé |
||||||
| |
-f CE = -mrL' ce travail est égal à la variation de l'énergie cinétique 0,5 mvE² -0,5 mv²C. vE² = v²C- 2rL' ou vC² = v²E+ 2rL' valeur minimale de la vitesse en C : vC² = 0,5² +2*0,032*400=25,85 et VC=5,08 ms-1. valeur maximale de la vitesse en C : vC² = 1,5² +2*0,032*400=27,85 et VC=5,28 ms-1.
|
||||||
|
|
|