| |
mouvement circulaire, tension d'un câble En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
|
mouvement circulaire |
Une demi-sphère creuse, d'épaisseur négligeable, de centre O et de rayon R repose par son sommet S sur un plan horizontal. Elle est maintenue fixe dans cette position. Un petit solide de masse m assimilable à un point matériel peut glisser sans frottement sur la face interne de la demi-sphère. On désigne par M sa position reperée par l'angle q. On communique à ce solide, à partir d'une position initiale M une vitesse V tangente horizontalement à la demi-sphère de module V tel qu'il décrive, d'un mouvement uniforme un cercle horizontal passant par ce point M, sur la face interne de la demi-sphère. 
|
|||||
| . . | |||||||
| |
accélération centripète a = v²/AM AM = R sinq. tan q = a / g-->a = g tan q d'où v²= g R tan q sinq = g R sin²q / cos q
si q = 60°, v²= 12 et v=3,46 ms-1.
vitesse angulaire (rad s-1)= vitesse (ms-1 ) divisée par AM(m) 3,46 /(0,8 sin 60)= 5 rad s-1.
|
||||||
|
bilan énergétique |
Je lache un bloc de masse 2500 kg depuis le haut d'une falaise mesurant 15m de haut. Le bloc est accroché au haut de la falaise par l'intermediaire d'un câble ayant les caractéristiques suivantes (diamètre=16 mm longueur= 5m et E= 11000daN/mm2).
corrigé |
||||||
| |
altitude zéro : +5 m par rapport au pied de la falaise en haut : énergie potentielle de pesanteur mgh=2500*9,8*10 =245 kJ altitude 5 m cable non tendu : énergie potentielle de pesanteur + énergie cinétique = 245 kJ 245 kJ doivent être absorbés par le câble sous forme d'énergie potentielle élastique. pour un allongement de 5 m : 245 000 = 0,5 *raideur *5² -->raideur =19600 N/ m tension maxi du câble : 19600*5=98 000 N ou 9800 daN
La tension maxi du cable est de 75 000 N --> allongement =75 000 / 19600 =3,82 m énergie potentielle élastique : 0,5* 19600*3,82² = 143 kJ énergie absorbée par le système : 245-143 =102 kJ
|
||||||
|
cinématique accélération th du centre d'inertie |
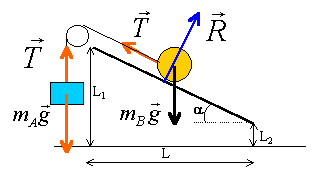
On relève les positions du centre d'inertie du solide B situé sur le plan.
mB=153 g ; L1=36 cm; L2=4 cm ; L=3,5 m. corrigé |
||||||
| |
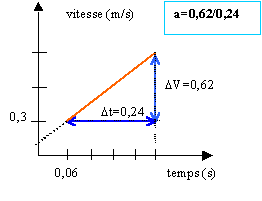
vitesse en A3:0,466 ms-1. vitesse en A4:0,625 ms-1. vitesse en A5:0,775 ms-1. vitesse en A6:0,933 ms-1. la vitesse augmente de 0,16 ms-1 toutes les 0,06 s --> a= 2,66 ms-2.
D'après le graphe, la vitesse en A1 est voisine de 0,1 m/s. Or v=2,66 t d'où la durée du parcours A0A1 voisine de 0,037 s La poulie ayant une masse négligeable A et B ont la même accélération. th. du centre d'inertie appliqué à B, projection sur un axe parallèle au plan dirigé vers le haut. -mB g sin a + T= mB a avec sin a =(0,36-0,04) / 3,5 = 0,091 T=mB (a+g sin a ) T=0,153(2,66+9,8*0,091)= 0,544 N th. du centre d'inertie appliqué à A, projection sur un axe vertical dirigé vers le haut. -mA g + T= mA a mA = T /(a+g)=0,544 /(2,66+9,8) = 44 g
|
||||||
|
|
|
||||||