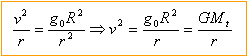Aurélie octobre 2000


devoirs en terminale S

satellite, th de l'énergie cinétique, th du centre d'inertie

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


1

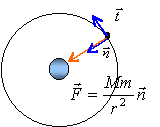
satellites et 3ème loi de kepler
G=6,67 10-11 S.I ; Rayon de la terre R=6400 km ; g0=9,8 m s-2.
  1. Donner l'expression du champ de gravitation à une altitude h.
  2. En déduire l'expression litérale de MT , masse de la terre en fonction de g0, R. Calculer MT.
  3. Un satellite de la terre, de masse m, considéré comme ponctuel, décrit une orbite circulaire de rayon R+h. (h : altitude) Dans le référentiel géocentrique, montrer que le mouvement est uniforme. On pose r=R+h.
  4. Donner l'expression de la vitesse en fonction de g0, r.
  5. Exprimer la période T du satellite en foction de r, Mt.
  6. Montrer que le rapport r3 / T² est constant.
  7. périodes et altitudes de quelques satellites de la terre.

vérifier que le rapport r3/T² st constant et en déduire la masse de la terre.

 

corrigé

.
.

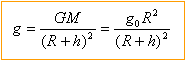
Masse de la terre : M = g0R²/G 

M=9,8 * (6,4 106)² / 6,67 10-11 = 6 1024 kg

l'accélération est centripète, la composante suivant l'axe t de la base de frenet est nulle, donc la norme de la vitesse est constante et le mouvement est uniforme.

ou bien une force perpendiculaire à la vitesse ne travaille pas donc l'énergie cinétique n'est pas modifiée .

vitesse : l'accélération normale est égale à v²/r.

période (s) fois vitesse (m/s) = circonférence de rayon r (m)

Tv=2pr ou T² v² = 4 p² r²

remplacer v² par l'expression ci dessus

attention distance en mètre et période en seconde

1013 = 6,6 10-11 Mt / 4p²

Mt = 4p²1024 / 6,67 = 5,91 1024 kg

 


2

un petit pendule, tension et vitesse

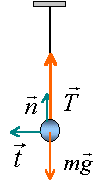
Une bille d'acier de masse m est suspendue en un point fixe par un fil inextensible de longueur L. Le pendule ainsi constitué est ecarté d un angle a0 de sa position d' équilibre puis abandonné sans vitesse initiale , il effectue alors des oscillations de part et d autre de sa position d'équilibre .

  1. A l'instant où la balle passe par sa position d'équilibre déterminer l'expression littérale de sa vitesse en appliquant le th de l'énergie cinétique . En déduire l' accélération normale de la bille.
  2. En appliquant le th du centre d'inertie montrer que l' accélération tangentielle est alors nulle .
  3. Exprimer la vitesse de la bille et la tension du fil lorsque celui ci fait un angle a avec la verticale.
corrigé


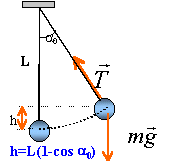
seul le poids travaille, la tension étant perpendiculaire à la vitesse.

au passage à la position d'équilibre, pendule vertical :

mgL(1-cos a0)=0,5 mv²

v²=2gL(1-cos a0)

accélération normale v²/L = 2g(1-cos a0)

au passage à la position d'équilibre accélération verticale car somme des forces vecteur vertical: donc pas d'accélération suivant l'axe t de la base de Frenet.

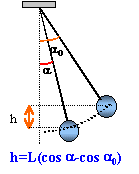
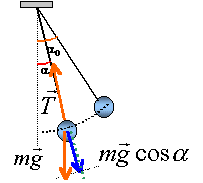
mgL(cos a-cos a0) = 0,5 mv²

v²= 2gL(cos a-cos a0)

T-mgcos a = mv²/ L

T = mgcos a +2mg(cos a-cos a0)

T = mg(3cos a-2cos a0)




retour - menu
à suivre