| |
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
| |
|
||||||
|
|
fréquence, période, longueur d'onde |
une radiation émise par une lampe à vapeur de lithium a une période de 1,533 10-15 s.
corrigé |
|||||
| |
fréquence = 1/1,533 10-15 =6,52 1014 Hz longueur d'onde (m) = célérité (3 108 m/s) fois période (s) l=3 108*1,533 10-15 =4,6 10-7 m = 456 nm (bleu violet) seule la fréquence reste constante dans divers milieux transparents, vitesse et longueur d'onde dépendent du milieu de propagation. |
||||||
|
réfraction dispersion |
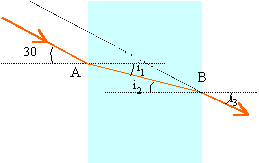
Un rayon lumineux monochromatique arrive sur une vitre faite de verre d'indice n =1,5 et d'une certaine épaisseur e. L'angle d'incidence est i =30°.
corrigé |
||||||
| |
i1=i2 angles alternes internes en b : 1,5 sin i2 = sin i3 donc i3=30° le rayon qui arrive et celui qui sort sont parallèles quel que soit l'indice du milieu constituant la vitre.
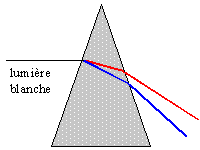
Une vitre ne disperse pas la lumière blanche alors que le prisme disperse cette lumière blanche
|
||||||
|
dispersion par un prisme |
corrigé |
||||||
| |
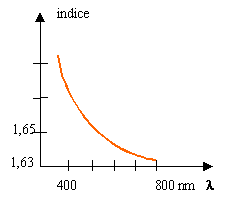
Le graphique donne respectivement n=1,68 et n=1,635. Pour la lumière jaune l'indice est proche de 1,65.
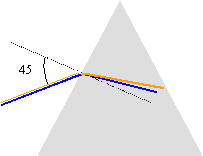
indice pour chaque radiation (lecture graphe) n1=1,675( bleu); n2=1,65 ; n3 =1,645(orange) . n air sin45 = 1,675 sin i1 i1 = 24,97 ° n air sin45 = 1,65 sin i2 i2 = 25,37 ° (écart 0,4 °) n air sin45 = 1,645 sin i3 i3 = 25,46 °(écart 0,1°) |
||||||
|
un disque opaque flotte... |
Un disque opaque de diamètre D=10cm flotte, immobile ,à la surface de l'eau d'un cristallisoir. La hauteur d'eau est H=20 cm. L' indice de l ' eau est n=1,33 .Un oeil est placé en O à la verticale du centre du disque et à une distance h = 10 cm au dessus de celui - ci .
corrigé |
||||||
| |
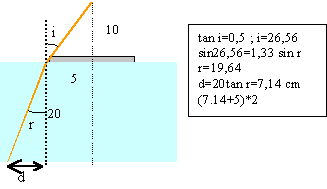
la partie masquée est un disque de rayon 12,14 cm |
||||||
|
un faisceau laser ... |
Un faisceau laser est envoyé sur un bloc de plastique transparent à faces paralléles d'epaisseur 5,00 cm. Le laser est positionné en L à 5,00 cm au dessus du bloc de plastique. Le faisceau arrive sur la face d'entrée du bloc avec une incidence de 60,0°. Le plastique a un indice de réfraction de 1,402 pour la lumiere de ce laser.
corrigé |
||||||
| |
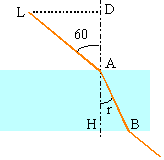
triangle LAD : cos 60 = AD / AL d'où AL =5/0,5 =10 cm. sin 60 =1,402 sin r sin r = 0,866/1,402 =0 ,617 r = 38,15°. triangle ABH : cos r = AH / AB d'où AB = 5 / 0,786 =6,36 cm. vitesse de la lumière dans le plastique = 3 108 / 1,402 = 2,14 108 m/s. durée du parcours LAB : 0,1 / 3 108 + 0,063 / 2,14 108 = 6,27 10-10 s. durée du parcours LC dans l'air : 0,08 / 3 108 = 2,66 10-10 s. durée du parcours CB dans le plastique : 0,08 / 2,14 108 = 3,74 10-10 s. |
||||||
|
|
|