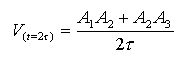| |
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||||||||||||||||||||||
| |
|
||||||||||||||||||||||||||
|
|
vitesse et référentiel |
Deux véhicules A et B assimilés à des points matériels se déplacent sur une même trajectoire rectiligne. Les mouvements sont uniformes dans un référentiel terrestre. VA=15 ms-1 et VB=20 ms-1. Représenter les vecteurs vitesses :
envisager les deux cas: les véhicules se déplacent dans le même sens ou en sens contraire. corrigé |
|||||||||||||||||||||||||
| |
dans un référentiel lié à A : A est immobile et B se déplace à 5 m/s dans le sens de A ou à 35 m/s en sens contraire.
dans un référentiel lié à B : B est immobile et A recule à 5 m/s ou se déplace à 35 m/s en sens contraire de B
|
||||||||||||||||||||||||||
| . . | |||||||||||||||||||||||||||
|
mouvement sur un plan incliné |
On lâche un palet sur une table à coussin d'air inclinée sur l'horizontale. On visualise les différentes positions du centre d'inertie du palet . (t=40 ms)
corrigé |
||||||||||||||||||||||||||
| |
la vitesse initiale est voisine de 1 m/s.
|
||||||||||||||||||||||||||
|
satellite géostationnaire |
Un satellite géostationnaire effectue dans le référentiel géocentrique un tour en un jour. Il est situé à l'altitude de 36000 km et le rayon de la terre est 6400 km.
|
||||||||||||||||||||||||||
| |
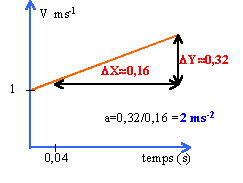
Il tourne dans le même sens que la terre . Il a la même vitessse angulaire que la terre. w(rad s-1)=2*3,14 / période ( s) 6,28 / (24*3600)= 7,26 10-5 rad s-1. vitesse (ms-1) = w(rad s-1)* rayon de la trajectoire (m) 7,26 10-5 *(36000+6400) 103= 3,078 km s-1. 800 / 3,078 = 260 s = 4 min 20 s |
||||||||||||||||||||||||||
| |
|
||||||||||||||||||||||||||
|
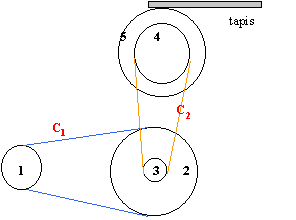
tapis roulant |
diamètres des poulies : d1=10 cm; d2=50 cm ; d4=30 cm; d5=35 cm .
corrigé
|
||||||||||||||||||||||||||
| |
1,5 = w5(rad s-1) *rayon poulie n°5(m) w5= 1,5/ 0,175 = 8,57rad s-1. d'où N5=8,57 / 6,28 = 1,364 tours par seconde. Les deux poulies 4 et 5 ont la même vitesse de rotation. De 2 poulies reliées par une courroie, la plus petite tourne le plus vite. vitesse de rotation et diamètre sont inversement proportionnels. N4 d4 = d3 N3 d3 =1,364 *0,3 / N3 calcul de N3 N1=24 tours / s N1 d1 = d2 N2 N2 = 24*0,1 / 0,5 = 4,8 tr / s Les poulies 2 et 3 ont la même vitesse de rotation. d3 =1,364 *0,3 / 4,8 =0,085 m ou 8,5 cm vitesses des courroies vitesse angulaire d'une poulie * rayon poulie 24*6,28*0,05 = 7,53 m/s pour C1. 8,57*0,15 = 1,28 m/s pour C2. |
||||||||||||||||||||||||||
|
Metz- Reims |
|
||||||||||||||||||||||||||
| |
110/3,6 = 30,55 m/s 130 /3,6 = 36,11 m/s équations horaires : d1=30,55 t d2 = 36,11 (t-900) origine des temps comptés depuis le départ de 1. durée du parcours : t1= 174000/30,55 = 1h 34 min 55 s arrivée à : 15h 34 min 55 s t2= 174000/36,11 = 1h 20 min 18 s arrivée à : 15h 35 min 18 s donc 2 ne rattrappe pas 1. 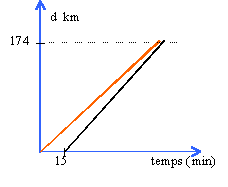
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||