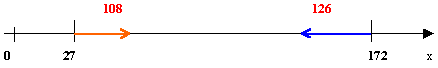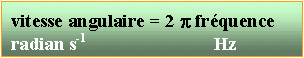Aurélie sept 2000


devoirs 1ère S : mouvement - ressort

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


1

mouvements

de 2 voitures

Deux automobilistes A et B se déplacent sur une autoroute rectiligne. Les équations horaires de leurs mouvements sont XA (t) = 108 t + 27 XB (t) = - 126 t + 172 où XA et XB désignent les abscisses des 2 véhicules A et B comptées à partir de la même origine d'un repère d'espace et exprimées en km et t la date exprimée en heures.

  1. Quelle est la distance qui sépare les deux véhicules à t = 0
  2. Les 2 véhicules vont-ils dans le même sens ?
  3. A quelle date se croisent-ils ou se dépassent-ils ?
  4. Déterminer l'abscisse de croisement ou de dépassement.
  5. Au moment du dépassement ou du croisement quelle distance ont ils parcouru. 
corrigé

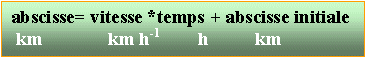
Un signe - devant la vitesse signifie que le véhicule B se déplace en sens contraire de l'axe.

La distance séparant A et B à la date t=0 est 172-27 = 145 km.

Lors du croisement les abscisses de A et B sont identiques

108 t + 27 = -126 t +172

t =( 172-27) / (108+126) = 0,619 h ou 31 min 11 s

abscisse du croisement : remplacer le temps par la valeur précédente dans l'une ou l'autre espression de l'abscisse.

108*0,619 +27 = 93,85 km

distance parcourues :

par A : 93,85-27 = 66,85 km

par B : 172-93,85 = 78 ,15 km
.
.
2

relativité du mouvement

Au cours d'un vol entre Paris et Toulouse, un Airbus, volant à V1 = 820 km/h par rapport au sol, suit la voie ferrée du T.G.V (supposée rectiligne) , la vitesse de croisière d'un T.G.V (allant de Toulouse vers Paris ) est V2 = 320 km/h par rapport au sol .On supposera les portions rectilignes et on prendra un repère d'espace x'x orienté de Paris vers Toulouse

  •  

  1. Quelle est la vitesse d'un chef de gare assis à son bureau par rapport à un passager assis dans l'Airbus
  2. Quelle est la vitesse de l'Airbus par rapport à un passager assis dans le T.G.V?
  3. Lorsque l'Airbus et le T.G.V se croisent quelle est la vitesse d'un passager assis dans le TGV par rapport à l'Airbus ?

corrigé


Le référentiel est le sol.

Dans ce référentiel le chef de gare est immobile alors que l'avion se déplace vers Toulouse à la vitesse de 820 km/h.

Pour un passager de l'avion le chef de gare et la gare se déplace vers Paris à la vitesse de 820 km/h.

Dans le référentiel lié au sol le train se déplace vers Paris à la vitesse de 320 km/h.

Pour un passager de l'avion, le train se déplace vers Paris à la vitesse de 820+320 km/h

Pour un passager du train, l'avion se déplace vers Toulouse à la vitesse de 820+320 km/h
3

système de poulies

Une poulie (P1) de rayon R1 = 300 mm entraîne par l'intermédiaire d'une courroie une poulie (P2) de rayon R2 = 100 mm . La poulie (P1) tourne à raison de n1 = 180 tours / mn.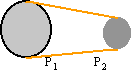

  1. Déterminer sa fréquence de rotation.
  2. Déterminer sa période.
  3. Déterminer sa vitesse angulaire w1.
  4. Déterminer la vitesse linéaire d'un point de la périphérie de la poulie ?
  5. Quelle est la vitesse linéaire des points de la courroie ?
  6. En déduire la vitesse angulaire w2 de la poulie (P2) ?
corrigé

180 tours par minute soit 3 tours par seconde; fréquence = 3 Hz

période : durée pour éffectuer un tour = 1/3 = 0,33 s

6,28*3 = 18,84 rad s-1.

18,84 * 0,3 = 5,65 m s-1.

Si la courroie ne patine pas, la vitesse d'un point de la courroie est 5,65 m s-1.

La poulie la plus petite tourne plus vite que la grosse. Le rapport des vitesses de rotation est l'inverse du rapport des diamètres.

le rapport de diamètres est 1/3. Donc

w2 = 3*w1 =56,5 rad s-1.

4

raideur d'un ressort

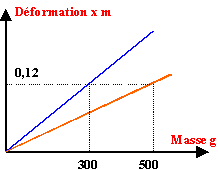
On considère deux ressorts à réponse linéaire, de longueur à vide lo = 30 cm, dont on veut déterminer expérimentalement les constantes de raideur k1 et k2.

  1. Faire l'inventaire des forces extérieures s'exerçant sur les 3 systèmes suivants
  • Le plateau + les charges
  • le ressort
  • plateau + charges +ressort
  1. Donner un exemple de 2 forces liées entre elles par le principe des interactions
  2. Montrer la relation m .g = k . x on rappelle g = 9,8 N.kg-1
  3. On obtient expérimentalement les 2 graphes ci-dessous (allongement x (en m) en fonction de la masse m (en g)). Déterminer les coefficients directeurs des 2 graphes
  1. En déduire les constantes de raideur k1 et k2 des 2 ressorts
  2. Déterminer la valeur de la masse m disposée sur le plateau lorsque la longueur du ressort n°2 (ressort ayant la plus grande raideur) est 37cm
  3. Quelles sont les longueurs respectives l1 et l2 des ressorts lorsqu'on exerce à l'extrémité de chacun une force F = 3,5N
    corrigé


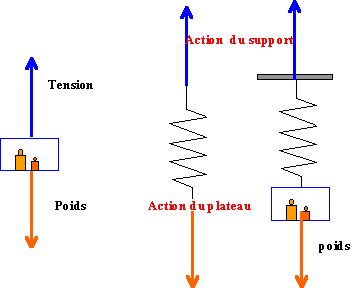
action du plateau sur le ressort et tension du ressort (ou action du ressort sur le plateau) sont liées par le principe des actions mutuelles.

A l'équilibre du plateau suspendu , le poids et la tension du ressort sont opposés

poids (N) = masse (kg) * 9,8

tension proportionnelle à l'augmentation de longueur du ressort (mètre) . La constante de proportionnalité est appelé raideur notée k en N /m.

mg = kx

coefficient directeur des droites :

0,12 /0,3 = 0,4 m kg-1.

0,12 /0,5 = 0,24 m kg-1.

raideur des ressorts (N m-1):

9,8 N/kg divisé par les valeurs précédentes (m /kg).

9,8 /0,4 = 24,5 N m-1.

9,8 /0,24 = 40,8 N m-1.

allongement du ressort : 37-30 = 7 cm = 0,07 m

tension : 40,8 *0,07 = 2,85 N

poids = m *9,8 = 2,85

m = 285 g

déformations des ressorts : tension / raideur

3,5 /24,5 = 0,143 m =14,3 cm --> longueur = 30+14,3 = 43,3 cm

3,5 /40,8 = 0,086 m =8,6 cm --> longueur 30+8,6 = 38,6 cm.




retour - menu
à suivre