Aurélie avril 2001


devoirs 1ère S : énergie mécanique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


1

un petit pendule...

Une petite bille de masse m=200g est accrochée à un point fixe O par un fil inextensible de masse négligeable et de longueur L=80 cm. On prendra g=9,8N.kg-1. On repère sa position par l'angle a que fait le fil avec la verticale passant par O.Tout en le maintenant tendu, le fil est écarté de sa position d'équilibre d'un angle a 1 = 30° et lancé avec une vitesse initiale v1 = 1,5 m.s-1. On néglige les frottements.

  1. Déterminer l'expression de l'énergie mécanique du système {bille en interaction avec la Terre } à l'instant initial. Calculer sa valeur.
  2. Montrer que l'énergie mécanique du système se conserve. Quelle est la vitesse de la bille lorsque le fil passe par la position verticale (a = 0°) ?
  3. Déterminer l'expression de l'angle maximum a m de remontée. Quel est le mouvement ultérieur du pendule ?
  4. Quelle la vitesse initiale v'1 devrait-on communiquer à la bille pour qu'elle arrive à la verticale (a = 180°) avec une vitesse v'2 = 5,0 m.s-1 (le fil restant toujours tendu) ? Donner son expression, puis calculer sa valeur. Quel est alors le mouvement ultérieur du pendule ?

corrigé


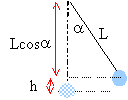
origine des énergies potentielles de pesanteur: le point le plus bas, correspondant à la position d'équilibre (a = 0)

au départ:

altitude : L- L cos a = 0,8 -0,8 cos 30 = 0,107 m.

énergie potentielle de pesanteur : mgh = 0,2*9,8*0,107 = 0,21 J

énergie cinétique : ½ mv² = 0,5*0,2*1,5² =0,225 J

énergie mécanique : 0,21+0,225 = 0,435 J.

la bille est soumise à 2 forces : son poids et la tension du fil.

Or la tension est constamment perpendiculaire à la vitesse : cette force ne travaille pas.

Seul le poids travaille puisque les frottements sont négligés.

En conséquence, l'énergie mécanique du système reste constante.

.
.

au passage à la verticale, l'énergie mécanique est sous forme cinétique

0,435 = 0,5 *0,2 v²

v² = 4,35 d'où v = 2,085 m/s.

au passage au point le plus haut , l'énergie mécanique est sous forme potentielle de pesanteur. Soit h maxi la hauteur maxi atteinte

0,435 = 0,2 *9,8 h maxi.

h maxi = 0,222 m

0,222 = 0,8 (1-cos amaxi)

1-cos amaxi =0,222 /0,8 =0,2775 d'où amaxi = 43,7°.

la bille rebrousse chemin et remonte de l'autre coté à la même hauteur (0,222 m) et ainsi de suite.

au passage à la verticale (position haute a=180°)

énergie potentielle de pesanteur : m g 2L

énergie cinétique ½m v'²

énergie mécanique : m(2gL+½v'²)

on part de la même altitude (a1= 30°) avec une vitesse v'd.

énergie potentielle départ : m g L (1-cos a1 )

énergie cinétique départ : ½ mv'²d.

énegie mécanique départ : m( g L (1-cos a1 ) +½v'²d)

conservation de l'énergie mécanique :

2gL+½v'² = g L (1-cos a1 ) +½v'²d

v'²d = v'² + 2gL[ 2 -(1-cos a1) ]= v'² + 2gL[ 1+cos a1 ]

5² + 2*9,8*0,8*(1+cos30)=54,26 d'où la vitesse initiale : 7,36 m/s.

puis la bille redescent de l'autre côté et continue d'effectuer des tours complets en l'absence de frottements.


à suivre ...
retour - menu
à bientôt ...