Aurélie dec 2000


devoirs 1ère S : mouvement uniforme, couples

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


1

le cycliste freine en descente
  1. Un homme sur une bicyclette descend une côte de 10% en freinant. Le système {cycliste-bicyclette} a une masse m=80kg et une vitesse constante v. la descente est rectiligne.
  2. Quelle est la nature du mouvement du centre d'inertie du système ?
  3. Faire le bilan et représenter les forces appliquées au système en les rapportant au centre d'inertie G.
  4. En utilisant le principe d'inertie, calculer la composante normale Rn de l'action de la route sur le système et l'intensité f des frottements.
corrigé

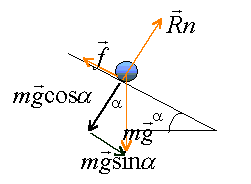
mouvement rectiligne uniforme, la norme de la vitesse est constante

En conséquence la somme vectorielle des forces appliquées au cycliste est nulle.

Rn = mg cos a

Rn =80*9,8*cos 5,7 = 780 N

avec tangente a voisin de sin a voisin de 0,1 et a voisin 5,7°.

f= mg sin a =80*9,8*0,1 = 78 N
.
.
2

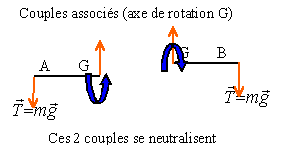
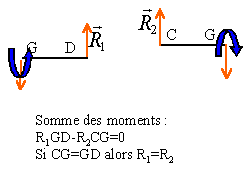
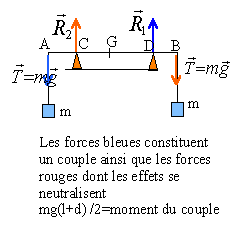
équilibre d'une poutre

Une règle horizontale de longueur L dont on néglige le poids, est en équilibre entre deux butées séparées par une distance d. Elle subit les forces de tension exercées par deux fils verticaux aux extrémités desquels sont accrochées deux charges de même masse m.

  1. Montrer que dans certaine condition les réactions des butées sur la règle ont la même valeur.
  2. Dans ces conditions en déduire que la règle est soumise à deux couples de forces.
  3. Exprimer leurs moments en fonction de m, g, de la longueur L de la règle et de la distance d.
  4. La valeur R des réactions des butées dépend elle de L et d ?
  5. On donne L= 50 cm, g = 9,8 N.kg-1, m = 100 g. Calculer R lorsque d prend les valeurs 5 cm, 10 cm, 20 cm.

corrigé


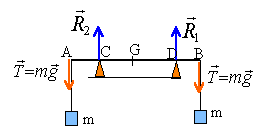
A l'équilibre la somme des vecteurs forces est nulle.

De plus la valeur (norme) des forces est la même quelle que soit la distance d et L

R1=R2=mg =0,1*9,8 =0,98 N

3

poulie à deux gorges

Deux filins sont enroulés sur une poulie à deux gorges(de rayon r1 et r2). L'un des filins est fixé à une charge de masse m; sur l'autre filin, on exerce une force F. L'action de l'axe de rotation sur la poulie est équivalente à une force R appliquée en un point de l'axe de rotation. Les poids de la poulie et des filins sont négligeables.

  1. Ecrire la relation entre F,r1,r2,m et g, à l'équilibre.
  2. La charge monte à vitesse constante Vb. Quelle relation existe-t-il entre Va et Vb?
  3. Quelle longueur L de corde a-t-on tirée en A pour un déplacement h de la charge?
  4. Quelle est la valeur de la force F à exercer sur le filin, en A, pour que la masse monte à la vitesse constante Vb?
  5. Montrer que F.L=m.g.h

     

corrigé


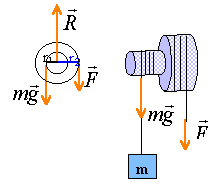
 l'action de l'axe n'a pas d'effet de rotation

effet de rotation (ou moment ) de la force F : + r2F

effet de rotation de la force mg : -mgr1.

si l'ensemble monte à vitesse constante alors les effets de rotation se neutralisent:

r2F-mgr1=0 (1)

la vitesse Va est la vitesse avec laquelle la corde enroulée sur la grande poulie se déplace.

écrire que les deux poulies ont la même vitesse de rotation w.

écrire que la vitesse de rotation est liée à la vitesse linèaire et au rayon par la relation :

w= Va / r2 = Vb / r1 .

ou bien Va r1 =Vb r2.(2)

pendant la durée t (s) :

longueur de corde divisée par durée = Va soit t =Va / L

hauteur fois la même durée = Vb

h*Va / L= Vb ou bien h Va = L Vb.(3)

(2) sécrit r1/ r2 = Vb / Va

(3) sécrit h / L = Vb / Va

d'où : r1/ r2 = h / L

(1) sécrit r1/ r2 = F / mg

h / L= F / mg ou bien FL = mgh

ce qui revient à écrire que le travail de la force F est égal en valeur absolue au travail du poids de la charge.


à suivre ...
retour - menu
à bientôt ...