Aurélie dec 2000


devoirs 1ère S : transfert d'énergie

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


1

le soleil, un réacteur nucléaire

On peut comparer le Soleil à un réacteur thermonucléaire transformant 564 000 000 t d'hydrogène en 560 000 000 t d'hélium à chaque seconde.

  1. Quelle est (en W) la puissance rayonnée par le Soleil?
  2. Quelle masse a-t-il perdue depuis qu'il rayonne (environ 5 milliards d'années)?
  3. Quelle fraction de sa masse cela représente-t-il?

    masse du soleil: M=2 1030 kg

    vitesse de la lumière: 3 108 ms-1.

corrigé

Dans une réaction nucléaire, une diminution de masse correspond à une libération d'énergie

D m* c²= énergie en joule

D m = 5,64 1011 -5,6 1011 = 4 109 kg à chaque seconde.

c² = (3 108)² = 9 1016 m² s-2.

puissance (watt) = énergie libérée à chaque seconde

3,6 1026 J / s (ou watt)

masse perdue depuis qu'il rayonne :

à chaque seconde 4 109 kg

durée : 5 109 *365*24*3600 = 1,57 10 17 s

masse perdue en 5 milliards d'années : 6,3 1026 kg

fraction de la masse du soleil :

6,3 1026 / 2 1030 = 0,03 %. 
.
.
2

chauffe-eau solaire
  1. Quelle énergie faut-il pour chauffer 100 litres d'eau de 25 à 75 degrés C? (l'énergie nécessaire pour élever de 1 degré Celcius 1 kg d'eau est 4,2 kJ).
  2. On utilise pour chauffer cette eau, un capteur plan recevant une puissance lumineuse de 1 kW et qui transforme à 50 % cette énergie en chaleur. Quel est le débit de l'eau dans le capteur, sachant qu'elle y pénètre à 25 degrés C et en sort à 75 degrés C.
  3. Combien de temps faut-il pour chauffer 100 litres d'eau?
corrigé

énergie nécessaire à chauffer 100 L d'eau de 25 à 75 °C :

100*4,2*(75-25) = 2,1 104 kJ.

0,5 kW ou kJ / s est utilisé au chauffage de l'eau.

0,5 = 4,18*(75-25)*débit massique (kg s-1)

débit massique = 2,4 10-3 kg / s ou 8,6 L / h

durée du chauffage :

100 / 8,6 = 11,6 h.
3

un autre chauffe eau

Sur la notice d'un petit chauffe-eau instantané on peut lire:

- puissance: 125 millithermie par minute (125 mth/min);

- débit: 5 litres d'eau par minute à 40 degrés C.

  1. Sachant qu'une millithermie par minute représente 4,18.103 joules par minute, à quelle température l'eau froide doit-elle entrer dans le chauffe-eau pour qu'elle ressorte effectivement à 40 degrés C? La masse volumique de l'eau vaut 1000 kg m-3 et sa capacité thermique massique c= 4,18.103J.kg-1.K-1.
  2. On règle le débit d'eau à 2,5 L/min; à quelle température sortira l'eau chaude sachant que l'eau froide arrive à la température trouvée dans la première question?

corrigé



 passage de millithermies au joujes :

125*4,18 103= 5,225 105 J / min = 522,5 kJ / min

5 * 4,18 * différence de température = 522,5

différence de température = 25° soit 40-25=15°C.

Le débit est divisé par 2 donc la différence de température va doubler soit 50°C

puis ajouter 15° pout trouver la température de l'eau chaude : 65°C.

 

4

champagne

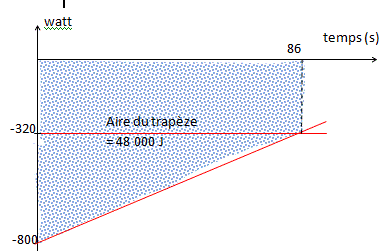
On cherche à refroidir une bouteille de champagne d'une température initiale T0=20°C à une température T=8°C.

On la place dans un mélange eau glaçon à 0°C. Quel temps faut il pour refroidir la bouteille de surface 500cm2 et de chaleur spécifique C= 4 kJ / K.

coeff d'échange convectif eau bouteille: 800W m-2 K-1.

corrigé


énergie cédée par la bouteille de champagne :

4*(20-8)= 48 kJ.

0,8 kW (ou kJ s-1) sont échangés par une surface de 1 m²

500 cm² =5 dm² =0,05 m²

0,05*800= 40W K-1 ( 40 W échangé par la bouteille pour une différence de température de 1°C ).

initialement la bouteille est à 20 °C et le mélange eau glaçon reste à O°C.

en conséquence durant la première seconde , 40*20 =800 J sont échangés.

finalement la bouteille est à 8°C et le mélange eau glaçon est à 0°C

en conséquence durant la dernière seconde , 40*8 =320 J sont échangés.


soit 48 000 = (800+320)*t / 2.
d'où t ~ 86 s.

Autre méthode.
Loi de Newton F = h S (T(t) - Tthermostat)= 40(T(t)-273).
h : coeficient de convection W m-2 K-1 ; S surface de contact ; T température en Kelvin.
F puissance perdue en W par convection.
dT(t) / dt = -a (T(t) - Tthermostat).
T(t) = Tthermostat+(T(0)-Tthermostat) exp(- hS/ C t).
h S / C = 800 x0,05 / 4000=0,01 s-1.
281 = 273+20 exp(- 0,01 t).
ln(8 /20)= -0,01 t ; t ~92 s.

5

transformer de la glace en vapeur d'eau
Quelle est la quantité de chaleur nécessaire pour convertir 10 g de glace à

-20°C en vapeur à 100°C ?

chaleur latente de fusion de la glace à °C : 335 kJ kg-1.

chaleur latente d'ébullition de l'eau :2 270 kJ kg-1.

capacité thermique massique kJ kg-1 K-1 :eau 4,2 ; glace 2,1.

corrigé



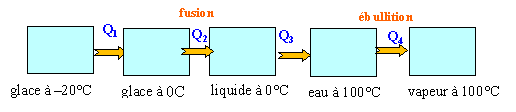
Q1 = 0,01 *2,1*(0 -(-20))= 0,42 kJ

Q2 : changement d'état ( fusion ) à température constante

335*0,01 =3,35 kJ

Q3 : 10 g de liquide se réchauffe de 0 à 100°C

0,01*4,2*100 = 4,2 kJ

Q4 : changement d'état ( ébullition ) à température constante

2 270*0,01 = 22,7 kJ

total : 30,67 kJ.

5

capacité thermique d'un calorimètre

Dans un calorimetre on place masse m1 d'eau. On attend l'equilibre thermique, puis on relève la température d'equilibre q1. On introduit une masse m2 de cuivre sortant d'une étuve thermostatée à la temperature q2. On attend l'équilibre thermique, on relève la température d'équilibre q3. On recomence l'expérience en changeant la masse m1, q1, q2 et q3.

  1. Trouver l'équation calorimétrique, équation reliant les capacites thermique massiques, la capacité

thermique Ccal du calorimetre et de ses accessoires, m1, q1, q2 et q3.

On a relevé les resultats suivants:

m1
m2
q1
q2
q3
epérience n°1
125 g
118 g
16,5
88
20,6
epérience n°2
100 g
118 g
20
75
23,7

  • écrire numériquement les deux équations reliant C cuivre et C calo.
  • en déduire C cuivre et C calo. C eau=4180 J kg-1 C-1
  • comparer ces résultat avec les valeurs C cuivre=380 J kg-1 C-1 et C calo= 160 J C-1.
corrigé


énergie gagnée par l'eau et le calorimètre :

(Ccal + m1 Ceau)( q3-q1)

énergie cédée par le cuivre :

m2 Ccuivre( q3-q2)

pas de pertes vers l'extérieur :

(Ccal + m1 Ceau)( q3-q1) + m2 Ccuivre( q3-q2) =0

application numérique :

(Ccal + 0,125*4180)(20,6-16,5)+0,118 Ccuivre(20,6-88)=0

(Ccal + 522,5)*4,1- 7,95 Ccuivre = 0

(Ccal + 522,5)*0,516 - Ccuivre = 0 (1)

(Ccal + 0,1*4180)(23,7-20)+0,118 Ccuivre(23,7-75)=0

(Ccal + 418)*3,7- 6,05 Ccuivre = 0

(Ccal + 418)*0,611 - Ccuivre = 0 (2)

(2) -(1) donne : 0,095 C cal =14,21 d'où C cal = 150 J C-1.

repport de cette valeur dans (1) :

(150+522,5)*0,516= C cuivre = 347 J kg-1 C-1

en accord à 10% près


De la vapeur d'eau, à la température de 100°C et sous la pression de 1 bar, est introduite dans un serpentin baignant dans de l'eau. La vapeur se condense.

  1. La vapeur reçoit-elle ou cède-t-elle de l'énergie au serpentin ?
  2. De l'eau dort du serpentin à la température de 80°C avec un débit de 0,25 L par minute. Calculer la puissance thermique reçue par le serpentin.

Données : Ceau=4,18 kJ.kg-1.°C-1 ; Leau= 2 260 kJ.kg-1.

corrigé
La vapeur se condense et cède de l'énergie au serpentin et à l'eau qui l'entoure.

débit : 0,25 L en 60 secondes soit 0,25 / 60 = 4,17 10-3 L/s

ou encore 4,17 10-3 kg/s.

On détermine l'énergie cédée par la vapeur d'eau puis par l'eau qui en résulte durant une seconde, ce qui revient à déterminer une puissance en watt ou joule / seconde.

D'une part la vapeur d'eau se liquéfie et donne de l'eau liquide à 100°C, en libérant 2660 kJ par kg de vapeur soit 2660* 4,17 10-3 = 11,1 kJ/s

d'autre part le liquide chaud se refroidit de 100°C à 80 °C libérant chaque seconde :

m Ceau Dq = 4,17 10-3 *4,18*20 = 0,35 kJ/s

soit au total : 11,1+0,35 = 11,45 kJ/s ou 11,45 kW.



10g de vapeur d'eau à 100°C sont injectés sur 50 g de glace à 0°C. Quelle sera la température à équilibre?

chaleur latente (kJ kg-1): eau:Lf=333,5 Lv=2258

Chaleur spécifique (kJ kg-1 K-1): eau=4,185 ; glace=2,093

corrigé
la vapeur se condense et donne de l'eau liquide à 100 °C

énergie cédée Q1 = 0,01*2258 = 22,58 kJ

le liquide se refroidit de 100 à q °C

énergie cédée : Q2 = 0,01*4,18*(100-q) = 4,18 -0,0418 q

total libérée par les corps chauds :Qchaud = 22,58 + 4,18 -0,0418 q = 26,76 -0,0418 q kJ

énergie nécessaire à la fonte de0,05 kg de glace à 0°C

0,05*333,5 = 16,67 kJ

l'eau de fonte se réchauffe de 0 à q °C

énergie mise en jeu : 0,05*4,18 q = 0,209 q

énergie totale gagnée par les corps froids : Qfroids=16,67 + 0,209 q

systéme supposé adiabatique : l'énergie cédée par les corps chauds est gagnée par les corps froids

26,76 -0,0418 q = 16,67 + 0,209 q

10,09 =0,251 q ;q =10,09 / 0,251 = 40,2 °C.



  1. Un pont métallique a une longueur initiale L0 =100 m à la température q0=0°C. Calculez l'augmentation de longueur DL qu'il subit lorsque sa température passe de q1= -20°C ( hiver) à q2=50°C ( été) . Le coefficient de dilatation linéaire du métal est a = 12 10-6 K-1.
  2. Un calorimètre contient une masse d'eau me=200 g dont la température initiale est q e=21,1 °C à l'équilibre thermique ( même température du calorimètre et accessoires). On introduit dans l'eau du calorimètre un échantillon d'aluminium de masse ma=199 g à la température q a=100,0°C. La température d'équilibre de l'ensemble, au bout d'un certain temps, se stabilise à q éq=33,0°C. Déterminer la chaleur massique ca de l'aluminium ( valeur en eau du calorimètre et accessoires m=40 g). ceau = 4185 J kg-1 K-1.
corrigé
Augmentation de longueur DL du pont :

Lq = L0(1+a(273+q))

Lq1 = L0(1+a(273+q1)) ; Lq2 = L0(1+a(273+q2)) ; DL = Lq2 -Lq1 =L0a[q2-q1]

DL =100*12 10-6 (50+20) = 0,084 m = 8,4 cm.

Chaleur massique ca de l'aluminium :

Energie Qc cédée par le corps chaud, l'aluminium : Qc =maca(q éq-q a)

Energie Qf gagnée par les corps froids, l'eau et le calorimètre : Qf =(me+m)ce(q éq-q e)

système adiabatique, sans échange de chaleur avec l'extérieur : Qc + Qf = 0

maca(q éq-q a) + (me+m)ce(q éq-q e) =0

ca = (me+m)ce(q éq-q e) / [ma(q a-q éq) ]

ca = 0,24*4185*(33-21,1) / (0,199*67)= 896 J kg-1 K-1.


Un appareil à cire est constitué d'une cuve en aluminium de masse 0,25 kg chauffé par une résistance thermo-régulée.La puissance électrique de cet appareil est 200 W. La cuve contient 500 g de cire, ressolidifiée après fusion et épousant la forme de la cuve. L'ensemble est à la température ambiante de 18°C. Cette cire dite "tiède" commence à fondre à 37°C. Le début de la fusion est observé au bout de 2 min 10 s.

  1. Calculer la capacité thermique massique, notée c, de la cire solide.
  2. Il faut encore attendre 12 min après le début de la fusion pour que la cire soit totalement fondue.
    - Cette cire n'étant pas un corps pur, que peut-on dire de la température en fin de fusion ?
    - Calculer la quantité de chaleur nécessaire à cette seconde étape.
    - En négligeant la quantité de chaleur absorbée par la cuve, déduire la quantité de chaleur nécessaire à la fusion de 1 kg de cette cire.
    Capacité thermiquemassique de l'aluminium : cAl=895 J kg-1 K-1.
corrigé
Capacité thermique massique, notée c, de la cire solide :

énergie électrique reçue en Dt =2 min 10 s = 130 s : Q1= P Dt =200*130 = 2,6 104 J

énergie reçue par la cire : Q= m c Dq =0,5 c* (37-18) = 9,5 c

énergie reçue par l'aluminium : Q' = m Al cAl Dq = 0,25*895*(37-18) =4,25 103 J

Q1 = Q+Q' ; 2,6 104 = 9,5 c + 4,25 103 ; c = ( 2,6 104-4,25 103)/ 9,5 = 2289 J kg-1 K-1.

Cette cire n'étant pas un corps pur, sa température de fusion n'est pas constante.

Quantité de chaleur nécessaire à cette seconde étape : P Dt = 200*12*60 = 1,44 105 J

Quantité de chaleur nécessaire à la fusion de 1 kg de cette cire : 2*1,44 105 = 2,88 105 J kg-1.



à suivre ...
retour - menu
à bientôt ...