concours technicien labo 01 sciences physiques et industrielles exercice suivant : électromécanique
1	mécanique des fluides
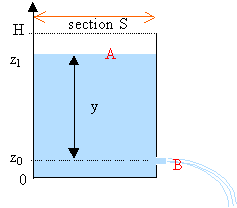
On considére un récipient de section constante, de hauteur H contenant de l'eau, considérée comme un liquide incompressible sans viscosité. L'accélération de la pesanteur est notég, la pression atmosphérique est notée pa.   Quelle relation lie la vitesse v0 de sortie de l'eau en B et la vitesse v = -dz/dt de descente de la surface libreA? Dans le cas où le fluide du récipient est stationnaire ( c'est le cas ici) , le théorème de Torriceli stipule que : ½ v0²+gz0 = v² + gzl. Déduire l'expression de v0 en fonction de S, s, y et g. - Le rapport S/s est inférieur à 0,01 , donner une valeur approchée de v0. - Exprimer alors v en fonction de S, s, y et g. corrigé
Le débit volumique en A surface libre et en B, orifice de sortie est constant. Un débit ( m3/s) est égal à une section (m²) fois une vitesse (m/s) v0 s = v S. ½ v0²+g z0 = ½v² + gzl avec zl = y+z0. ½ v0²+g z0 = ½(v0s/S)² + gy +gz0. ½ v0²= ½v0²(s/S)² +gy v0²(1 -(s/S)²)= 2g y v0² = 2gy / (1 -(s/S)²) si s/S inférieur à 0,01, s²/S² est inférieur à 10-4 et v0² voisin de 2g y. Dans ce cas v = racine carrée (2gy) s/S.
2	la clepsydre : horloge à eau des anciens
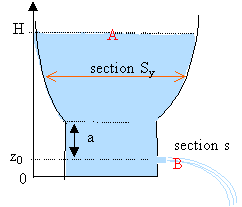
Dans l'exercice précédent la vitesse de descente de la surface libre décroît avec y. la hauteur de l'eau dans le récipient ne donne pas une valeur convenable du temps . On va y remédier en modifiant la forme du récipient. Le récipient reste cylindrique mais sa section varie. Exprimer la section S(y) en fonction de la section Sa (section constante de la partie inférieure), y et a pour que la vitesse de descente du liquide soit proportionnelle au temps. Sa est un disque de rayon 12 cm et a =10 cm. Quels doivent être les rayons des sections correspondant à y =20 cm et y = 40 cm. corrigé D'après la question précédente v² = 2gs² y/ S². Cette vitesse est indépendante de y si Sy est de la forme S²y = k y (avec k=constante) en particulier lorsque y = a, cette section vaut S²a= k a d'où S²y = y / a * S²a. application numérique : Sa = 3,14 *0,12 ² = 0,0452 m² Sa / a = 0,0452 / 0,1 = 0,452 m S²y = 0,452 y. si y= 0,2 m , S=0,0904 m² et le rayon vaut : racine carrée (0,0904/3,14) = 0,17 m. si y= 0,4 m , S=0,1808 m² et le rayon vaut : racine carrée (0,1808/3,14) = 0,24 m.
3	la clepsydre améliorée
Le niveau de l'eau baisse régulièrement tant que y reste compris entre les valeurs H et b. La section S du récipient est constante. Le petit tube permet à l'air extérieur de rentrer dans le récipient lorsque le niveau de l'eau descend. Juste après la fermeture du bouchon B, on admet qu'il reste un peu d'air dans la partie supérieure du récipient et que les niveaux de l'eau dans le tube et la clepsydre sont les mêmes. 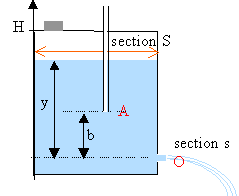Que se passe t'il par la suite lorsque l'eau s'écoule par l'orifice O? Quelle est la pression au point A, extrémité inférieure du tube lorsqu'elle est stabilisée? Le théorème de Torricelli s'applique entre le point A et le point O. Expliquer alors pourquoi le niveau de l'eau descend réguliérement dans la clepsydre? corrigé Lorsque le liquide commence à s'écouler par l'orifice O, le niveau de l'eau baisse dans le récipient : la pression de l'air situé à la partie supérieure du récipient, initialement à la pression atmosphérique, va décroître. L'air pénètre dans le petit tube et repousse le liquide jusqu'en A. pression en A= pression atmosphérique = pa autre expression : r g (y-b) pression exercée par la colonne de liquide de hauteur y-b à laquelle il faut ajouter la pression p de l'air situé au dessus de ce liquide. Cette valeur p est très inférieure à r g (y-b) car le volume laissé libre par l'écoulement de l'eau est grand devant le volume d'air initial emprisoné) (r est ma masse volumique de l'eau) pa -p =r g (y-b) soit g (y-b) voisin de pa / r. th de Torricelli entre les point A et O: ½ v0²+g z0 =½ v² + gzA avec zA = y-b+z0. ½ v0²= ½ v² + g (y-b) = ½ v² + pa / r. v² = v0² + pa / r. avec v S = v0 s (conservation du débit) La vitesse de descente est donc constante. retour - menu