concours technicien labo 2000 sciences physiques et industrielles exercice suivant : électrotechnique
1	accélération de la pesanteur
On désigne par G la constante de gravitation (G= 6,67 10-11 SI) et on considère un système de deux points matériels A1 et A2 de masse m1 et m2 dans un repère galiléen R tels que A1A2=d. Exprimer la force F12 ( expression vectorielle) que A1 exece sur A2 en fonction de m1, m2 ,G, d et du vecteur A1A2. A1 est fixe dans R et A2 mobile n'est soumis qu'à l'action de A1. Donner l'expression du vecteur accélération a2 correspondant au mouvement que prend A2. On considère un point matériel A de masse m, situé à la surface de la terre considérée comme sphérique, de masse M et de rayon R. L'altitude de A est négligeable devant R.On ne tient pas compte de la rotation de la terre autour de son axe SN, autrement dit, on considère tout référentiel lié à la terre comme galiléen. Caractériser le vecteur accélération Gg que prend le point matériel lorsqu'on le lâche . M=5,98 1024 kg et R= 6,37 103 km. 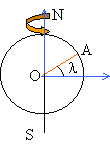La terre accompli un tour sur elle même en 0,997 jour soit 8,61 104 s. Déterminer la valeur de sa vitesse angulaire W. Du fait de la rotation de la terre autour de son axe SN, un référentiel lié à la terre ne peut pas être considéré galiléen : dans un tel repère un point matériel A, lorsque sa vitesse est nulle, est soumis à une force d'inertie Fi que l'on explicitera.. On exprimera sa norme en fonction de m, W et l la latitude . Les autres caractéristiques, direction et sens seront précisés sur un schéma. Lorsqu'on le lâche, sans vitesse initiale, à la surface de la terre, toujours parfaitement sphérique, le point matériel A prend une accélération caractérisée par le vecteur G, somme du vecteur Gg et d'un autre vacteur Gi . Donner l'expression de Gi et donner sa valeur maximale Gi0. On note g la norme du vecteur G. Déduire de la question précédente l'expression de g² en fonction de Gg , Gi0 et l. Montrer que l'on peut écrire avec une très bonne approximation que g = Gg - Gi0 f(l) où f(l) est une fonction de la latitude l que l'on précisera. En déduire la valeur de g pour l =45°. On note a l'angle entre les vecteurs G et Gg . 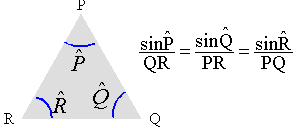Sachant que dans un triangle PQR on peut écrire : Etablir une relation entre a, l, Gg et Gi0 . Préciser les valeurs de a pour l =0, l =45°, l =90°. corrigé
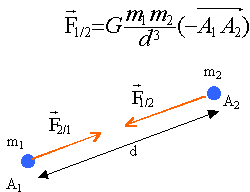
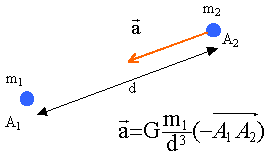
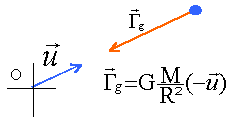
force de gravitation, toujours attractive, proportionnelle aux masses, inversement proportionnelles au carré de la distance. accélération centripète, dirigée vers le point fixe A1. le vecteur accélération est dirigé vers le centre de la terre . attention R en mètre R= 6,37 106 m Gg = 6,67 10-11 * 5,98 1024 / (6,37 106)2 = 9,83 m/s². vitesse angulaire de la tere : W = 2p / 8,61 104 = 7,3 10-5 rad /s. 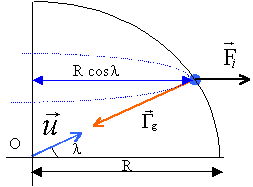force d'inertie centrifuge : Fi = mW²Rcosl. et Gi = W²Rcosl la valeur maximale correspond à une latitude l=0 : Gi 0=(7,3 10-5 )²* 6,31 106 = 3,36 10-2 m/s². 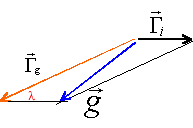g² = Gg ² +G ²i 0 -2Gi 0Gg cosl. 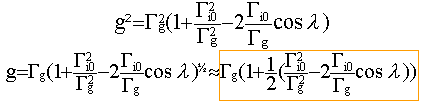g² = Gg ² (1+G ²i 0 / G2i 0 -2 Gi 0 /Gg cosl.) g = Gg - Gi 0 ( cosl -½ Gi 0 / Gg ). 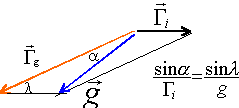sin a = 1/g ( W2Rcosl sinl ) = 1/(2g) W2R sin(2l) avec g = Gg-Gi0 f(l) l=0 a=0 l=45 a= 6 ' (minute d'angle) ou 0,0017 rad l=90 a=0 retour - menu