concours kiné (physique)
1	gravitation et satellite
Au cours de son exploration du système solaire, une sonde Voyager, de masse M = 2l00 kg, s'est approchée d'une planète notée A. On a mesuré à deux altitudes différentes comptées à partir du sol de cette planète la force de gravitation exercée par celle-ci sur la sonde soit: altitude z1 = 8 499 km F1 =13 236,51 N altitude z2 = 250 000 km F2 =189,25 N Données : masse de la Terre: MT = 5,98. 1024 kg ; Cte de gravitation K= 6,67. 10-11 Masses des planètes du système solaire: (la masse de la Terre étant prise égale à l'unité) Terre mercure vénus mars jupiter Saturne Uranus Neptune Lune 1 0,056 0,817 0,11 318 95,2 14,6 17 0,012 Parmi les unités écrites ci-dessous, laquelle convient pour exprimer le champ de gravitation? N / m ; m . s² ; m / s ; N / kg ; kg / N ; kg / m² ; kg / m² ; m² / s² ; kg /m Calculer le diamètre moyen de la planète A.(unité: 103 km) 50,5 ; 48,6 ; 12,1 ; 6,77 ; 138 ; 11,4 ; 4,88 ; 3,48 Quelle est l'intensité du champ de gravitation au niveau du sol de la planète A? (unité S.I) 1,66 ; 3,78 ; 8,62 ; 22,93 ; 11,48 ; 9,05 ; 7,84 ; 2,57 Quel est le nom de la planète A? mercure ; vénus ; lune ; jupiter ; saturne ; mars ; uranus ; neptune La planète A possède un satellite de rayon R =1350 km dont la période de révolution autour de A (sur une trajectoire supposée circulaire) vaut TS = 5 j 2l h 03 min. calculer la distance séparant le centre du satellite au centre de la planète A (unité 103 km) 18,8 ; 188 ; 353,8 ; 419,7 ; 253,8 ; 92,6 ; 543,6 ; 612,5  corrigé
il suffit de penser à : P = mg poids(N) = masse (kg) fois accélération de la pesanteur (m/s² ou N/kg) champs et forces sont proportionels. La cte de proportionalité est la masse du satellite. champ à une altitude h :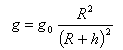 d'où F1 * (R+h1)² = F2 * (R+h2)² (forces en N et distance en m) R= 24,26 103 km D=48,52 103 km champ au sol : g0= g (R+h)²/R² et g= Force/Msatellite g0= 11,5 ms-2. masse planète en kg et rayon planète en m. d'où masse planète = 1,015 1026 kg rapport des masses de cette planète à celle de la terre :(diviser par la masse de la terre le résultat précédent) : 17 lire dans le tableau ci dessus : neptune. 3ème loi de képler : période en seconde, distance en mètre, masse en kg. R+h = 353,7 103 km.  retour - menu
2	énergies potentielles et cinétique
Un sportif de masse m = 75 kg effectue un saut à l'élastique en se lançant sans vitesse initiale d'un point A d'un pont situé au dessus d'une vallée. L'élastique a une longueur à vide AB = 23 m. La masse de l'élastique est négligeable. Au cours de la chute l'élastique se tend à partir du point B jusqu'au point C situé à 38 m au dessous du point A. On prendra le point A comme origine des altitudes et des énergies potentielles de pesanteur. L'axe des altitudes est orienté vers le haut. On ne considérera les forces de frottements qu'à partir de dernière question. g = 9,8 m /s² Calculer la vitesse du sauteur au point B. (unité: m / s) 4,61 ; 12,34 ; 21,23 ; 29,40 ; 124,6 ; 36,05 ; 252,4 ; 450,7 Calculer l'énergie mécanique du système ( Terre - sauteur - élastique) au point B. (unité: kJ) 16,9 ; 0 ; 33,8 ; 12,5 ; -12,5 ; 22,6 ; -16,9 ; -33,8 Calculer la constante de raideur k de l'élastique. (unité: N / m ) 64,6 ; 38,7 ; 98 ; 124,4 ; 158,4 ; 188,0 ; 206,4 ; 248,3 Calculer la vitesse du sauteur lors de sa première descente quand il passe à 10 m au dessous du point B. (unité: m / s ) 315,8 ; 12,6 ; 3,8 ; 22,3 ; 31,1 ; 47,6 ; 17,8 ; 108,4 En réalité au cours de la descente, du point B au point C, 13% de l'énergie élastique due à l'étirement de l'élastique est convertie en chaleur à cause des frottements. Les frottements dus à l'air seront négligés. Calculer la valeur réelle de la constante de raideur k. ( unité : N / m ) 78,4 ; 49,9 ; 115,0 ; 143,0 ; 182,1 ; 285,4 ; 216,1 ; 108,4  corrigé
énergie mécanique en B = énergie mécanique en A = 0 (départ sans vitesse et origine de l'énergie potentielle de pesanteur) 0,5 mVb² + mg hB=0 avec hb=-23 Vb² = 2ghb et Vb=21,23 ms-1. En absence de frottements l'énergie mécanique se conserve. en A elle est nulle en B aussi. En C, point le plus bas, la vitesse est nulle et l'élastique est tendu. L'énergie mécanique se trouve sous forme potentielle de pesanteur et potentielle élastique. 0,5 k x² + mghC=0 avec hC=-38 et x=38-23 = 15 k= 248,3 Nm-1. à 10 m en dessous de B, l'énergie est sous forme cinétique et potentielles de pesanteur et élastique 0,5 mv² + mgh+ 0,5 kx1²=0 avec m en kg, h=-33 et x1=10 v= 17,77 ms-1. exprimons l'énergie potentielle élastique en fonction de la raideur précédente et de la nlle raideur k1: 0,87 *0,5kx²=0,5k1 x² k1=216 Nm-1. retour - menu
3	calorimètre : transfert d'énergie sous forme de chaleur
On introduit dans un calorimètre de capacité thermique C =250 J.K-' un volume V1 =500 mL d'eau. Après agitation, la température d'équilibre de l'eau vaut q1 = 28,2 °C. Le calorimètre est considéré comme parfait. Données: capacité thermique massique de l 'eau liquide : 4185 J / (kg . K) capacité thermique massique de la glace : 2100 J / (kg . K) chaleur latente de fusion de la glace : 335 kJ / kg capacités thermiques massiques de métaux ou alliages en J / (kg . K) Plomb: 129 ; Cuivre: 388; Laiton: 370 ; Aluminium: 897 ; Argent: 235 ; Zinc: 399 ; Fer: 449 ; Titane: 523 On souhaite refroidir ce volume V1 d'eau afin que sa température finale soit q 2 = 10 °C. Calculer la masse minimale de glace, prise dans un congélateur à la température q3 = 18 °C qu'il faut introduire dans le calorimètre. (unité: g) 190,4 ; 102,8 ; 88,0 ; 72,5 ; 54,4 ; 48,2 ; 39,8 ; 18,5 On introduit dans le calorimètre contenant le volume V1 d'eau à la température q1 (conditions initiales ) un cylindre de métal de masse m =180 g sorti d'un four à la température q3 = 85,°C. Après agitation et retour - menu à l'équilibre, la température de l'eau dans le calorimètre vaut q4 =30,1 °C. Calculer la quantité de chaleur reçue par l'eau du calorimètre au cours de cette opération. (unité: kJ) 2,761 ; 3,082 ; 3,976 ; 4,451 ; 12,620 ; 54,582 ; 76,680 ; 114,98 Trouver le nom du métal Plomb ; Aluminium ; Cuivre ; Argent ; Zinc ; Laiton ; Fer ; Titane Pendant combien de temps faudrait-il faire passer un courant d'intensité constante I = 1,4 A dans une résistance R de valeur 30 ohms plongeant dans l'eau du calorimètre pour obtenir une élévation de la température de q1 à q4 (unité s) 76 ; 67 ; 92 ; 105 ; 122 ; 140 ; 172 ; 59 Parmi les propositions suivantes lesquelles sont VRAIES?: a- l'énergie totale d'un système isolé demeure constante b- tous les points d'un système en équilibre thermique ne sont pas obligatoirement à la même température c- un transfert d'énergie par chaleur ne produit pas toujours une modification de température a et c ; a et b ; a seule ; b seule ; b et c ; c seule ; toutes ; aucune  corrigé
Energie cédée par l'eau et le récipient S mc Dq = (250+4185*0,5)*18,2 = 42 633 J (1) Energie cédée par m kg de glace : pour passer à 0°C : 2100 m *18 fusion à 0°C : m*335 000 l'eau de fonte se réchauffe : m*4185*10 total : 2100 m *18+m*335 000+m*4185*10 (2) L'énergie cédée par les corps chauds et gagnée par la glace :(1)=(2) m= 102,9 g. Energie gagnée par l'eau du calorimètre : 0,5*4185*1,9 = 3,975 kJ. Energie gagnée par le calorimètre : 250*1,9 = 0,475 kJ. Energie cédée par le métal : 0,18 * cmétal *54,9 3975 + 475 = 0,18 * cmétal *54,9 cmétal =450 Jkg-1K-1. fer. Energie électrique = Ri² t. intensité en ampère, t en seconde ,R en ohm, énergie en joule 3975+475 =30*1,4²*temps 75,7 s. la proposition b est fausse. c: élévation de température ou changement d'état à température constante. retour - menu
4	dipoles (RC) ; (RL) ; (RLC)
Un condensateur de capacité C inconnue est initialement chargé sous une tension UPN = 8 V On étudie d'abord la décharge de ce condensateur dans un conducteur ohmique de résistance R1 inconnue. La constante de temps est t1=1,8 ms On recommence la même expérience en remplaçant le conducteur ohmique de résistance R1 par un autre conducteur ohmique de résistance R2 inconnue elle aussi .La constante de temps est t2=2,7 ms On monte ensuite les deux conducteurs ohmiques en série dans un circuit alimenté par un générateur de tension continue de f.e.m E = 23 V et de résistance interne négligeable .On lit I = 23 mA sur l'ampéremètre branché dans le circuit. Calculer la valeur de la résistance R1. (unité: kW ) 0,25 ; 0,40 ; 0,60 ; 1,00 ; 1,25 ; 1,4 ; 0,80 ; 0,16 Calculer la valeur de la capacité C. (unité: µF) 2,4 ; 3,5 ; 4,5 ; 5,4 ; 6,5 ; 7,6 ; 8,5 ; 10,2 Calculer l'énergie apparue sous forme de chaleur dans le conducteur ohmique de résistance R2 à la date t =3,0 ms. (unité: mJ) 0,016 ; 0,048 ; 0,24 ; 0,48 ; 0,13 ; 0,18 ; 1,14 ; 1,48 On branche maintenant aux bornes d'un générateur G de tension créneaux une bobine d'inductance L, de résistance r négligeable, en série avec le conducteur ohmique de résistance R2. Tension maximale aux bornes de la résistance R2 = 7V .La constante de temps est t2=2,7 ms. Calculer la valeur de l'inductance L de la bobine. (unité: mH) 270 ; 360 ; 87 ; 480 ; 160 ; 580 ; 680 ; 760 Quelle serait la fréquence propre du circuit composé des dipôles R1, L, C utilisés précédemment et montés en série? (unité : Hz) 1083 ; 680,5 ; 242,0 ; 68,1 ; 1720 ; 172 ; 331,4 ; 108,3  corrigé
U = (R1+R2) I tension (volt), résistances (ohms), intensité (ampères) R1+R2= 1000 (1) constante de temps du dipole R1 C : R1C=1,8 10-3 s constante de temps du dipole R2 C : R2C=2,7 10-3 s d'où R1/ R2= 1,8/2,7 = 2/3 (2) La résolution de ces 2 équations donnent : R1= 0,4 kW. C= 1,8 10-3 / 400 = 4,5 mF La tension au bornes du condensateur à une date t=3 ms, voisine de la cte de temps du dipole R2 C est voisine de 36,7 % de sa valeur initiale soit 8*0,367 = 3 V. Energie stokée par le condensateur: 0,5 CU² au départ : 0,5*4,5 10-6*8²= 1,44 10-4 J à t=3ms : 0,5*4,5 10-6*3²= 2,02 10-5 J énergie perdue , dissipée dans la résistance 1,24 10-4 J= 0,124 mJ constante de temps du dipole R2 L : L/R2 = 0,8 10-3 s L= 0,8 10-3 *600 = 0,48 H. période propre du dipole RLC: T en seconde, L en henry et C en farad T = 9,2 10-3 s fréquence = 1/ 9,2 10-3 = 108,3Hz. retour - menu