|
physique
|
||||||
|
chaîne énergétique |
|
|||||
|
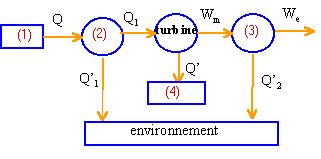
(2) réacteur, convertion d'énérgie nucléaire en chaleur (3) alternateur, conversion d'énergie mécanique en énergie électrique (4) condenseur, réservoir d'énergie 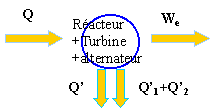
énergie(J) produite à chaque minute =puissance (W) * temps (s) We =800 106 *60 = 4,8 1010 J énergie mise en jeu : Q = 4,8 1010 / rendement de la chaîne 0,32 Q= 15 1010 J 15 1010 = Q'+Q'1+Q'2+We soit Q' = 7,62 1010 J 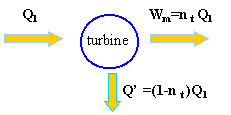
7,62 1010 = (1-0,43) Q1 Q1 = 13,36 1010 J Wm = nt * Q1=0,43 *13,36 1010 =5,74 1010 J 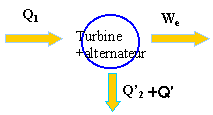
Q1 = We + Q' +Q'2. Q'2=(13,36 -4,8 -7,62) 1010 = 0,94 1010 J
|
||||||
|
frottements négligés |
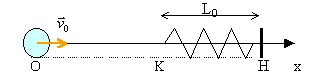
corrigé |
|||||
|
durée : t0 =1,95 / 0,3 =6,5 s. Puis le ressort se comprime ; l'énergie cinétique de la balle est convertie en énergie potentielle élastique (origine K : ressort non déformé, abscisse x0). A la date t : 0,5 mv0² = 0,5 mv² +0,5 k(x-x0)² dériver par rapport au temps : 0=0,5m*2 v v' +0,5k*2 x' (x-x0) avec v = x' et v' = x" diviser par v : mx" + k (x-x0)=0 avec x"= (x-x0)" équation différentielle du mouvement d'un oscillateur harmonique de pulsation w telle que : w²=k / m d'où w = 10 rad s-1. à t=t0, x=x0=OK x0 = A cos j + B. A : amplitude positive et B =OK donc j = p/2 ou -p/2 dériver x(t) pour avoir l'expression de la vitesse : v(t) = -Aw sin (w(t-t0)+j) à t=t0, v = v0. v0= -Aw sin j. A positif donc j =-p/2 donc A = 0,3 / (10 *1) =0,03 m x(t) =0,03 cos(10(t-t0)-p/2)+1,95.
à t = tM, toute l'énergie est sous forme potentielle élastique et la déformation du ressort comprimé est 0,03 m. xM=1,98 m soit tM-t0 = 1/4 période de l'oscillateur = 0,25 T avec T= 2p/w= 0,628 s. tM-t0 = 0,628 /4 = 0,157 s tM=6,657 s. une autre méthode : 1,98 = 0,03 cos(10 (tM-t0) -p/2)+1,95 1 = cos(10 (tM-t0) -p/2) 10 (tM-t0) -p/2 =0 10 (tM-t0) =p/2 tM-t0 =p/20 = 0,157 s
|
||||||
|
frottements non négligés |
|
|||||
|
0,5 mvK²-0,5 mv0² = -f OK vK² = v0² - 2f OK /m vK = 0,11 m s-1.
appliquer à nouveau le théorème de l'énergie cinétique entre K et O' (arrêt) 0-0,5 mvK² = -f O'K O'K = 0,5 mvK² / f = 0,5*0,1*0,11² / 2010-3 = 0,3025 m OO'=1,65 m. |