d'après concours Kiné berk sur mer 2000 exercice suivant : questionnaire chimie
1	lancer du poids
Au cours d'un championnat un athlète remporte l'épreuve de lancer de poids avec un jet à x1=19,27 m. Le poids a une masse m=7,26 kg . La trajectoire part d'un point A situé à une hauteur h=1,8 m . On assimilera le projectile à un solide ponctuel et on néglige l'action de l'air g=9,81 ms-2. Etablir l'équation cartésienne de la trajectoire Calculer la vitesse initiale si a=45 °. En déduire la hauteur maximale atteinte Donner les caractéristiques du vecteur vitesse en C corrigé
trajectoire et vitesse initiale : vecteur accélération ( 0 ; -g) vecteur vitesse initiale ( v0cos a ; v0 sin a) vecteur position initiale : ( 0 ; h) vitesse à une date t , primitive de l'accélération :( v0cos a ; -gt+v0 sin a) position à une date t, primitive du vecteur vitesse ( x= v0cos a t ; y = -½gt² + v0 sin a t +h) trajectoire : y = -½g x² /(v0cos a)² + x tan a +h au point d'impact x=19,27 m et y=0 0 = -4,9 *19,27² /(v0cos45)² +19,27 +1,8 d'où v0 = 13,14 m/s altitude maxi : écrire que la composante verticale de la vitesse est nulle : -gt + v0 sin a=0 t = v0 sin a / g = 13,14 sin 45 / 9,8 = 0,948 s repport dans l'expression de y : -4,9 *0,948² + 13,4 *sin 45 *0,948 +1,8 h maxi voisine de 6,4 m. vitesse au point d'impact : à quelle date passe t-on en C ? 19,27 = 13,14 cos 45 t d'où t =2,07 s. repport dans l'expression du vecteur vitesse abscisse : 13,14 cos 45 = 9,3 ordonnée : -9,8*2,07+13,14 sin 45 = -11 norme de la vitesse : racine carrée (11²+ 9,3² )= 14,4 m/s inclinaison sur l'horizontale : tan b = -11 / 9,3 =-1,18 et b = - 49,8 °.
2	oscillateur mécanique
Un oscillateur est constitué par un solide S de masse M, accroché à l'extrémité d'un ressort à spires non jointives de masse négligeable et de constante de raideur k. Le solide s oscille sans frottement suivant une table horizontale. On repère la position à l'instant t du centre d'inertie de S par l'abscisse x sur un axe horizontal dont l'origine correspond à la position du centre d'inertie au repos. Un dispositif permet d'enregistrer les variations de x en fonction du temps (graphe 1) et les variations de la vitesse en fonction du temps (graphe 2). 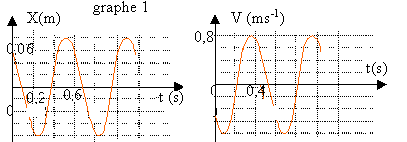Déterminer graphiquement la période propre T0 de l'oscillateur. En déduire la pulsation . Sachant que l'énergie mécanique de l'oscillateur est 70,4 mJ, calculer la constante de raideur k et la masse du solide . Préciser les conditions initiales (abscisse et vitesse) du mouvement. Etablir l'équation horaire du mouvement. Déterminer par le calcul la vitesse à t=0,5 s. Comparer à la valeur lue sur le graphique. corrigé
période (lecture graphe) voisine de 0,6 s; fréquence = 1/0,6 = 1,666 Hz pulsation w = 2p fréquence = 6,28*1,666 = 10,46 rad /s. l'énergie est sous forme potentielle élastique lorsque l'absicce est maximale, égale à l'amplitude :a=0,08 m( graphe1) 0,0708 = ½ k a² =0,5 *k*0,08² d'où k=22 N/m. w ²= k/m d'où m =22 /10,46² = 0,2 kg. conditions initiales (lectures graphes): x0 =0,06 m et v0 = -0,55 m/s. x(t) =0,08 cos(10,46 t+ j) à t=0 : 0,06 = 0,08 cosj. d'où j= 0,72 rad. x(t) =0,08 cos(10,46 t + 0,72) vitesse, dérivée de l'abscisse par rapport au temps v(t) = 0,08*(-10,46) sin(10,46 t + 0,72) v(t=0,5 )= -0,08*10,46 sin (10,46*0,5 +0,72) = 0,3 m/s. retour - menu