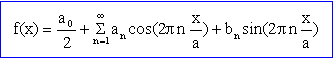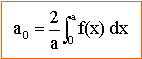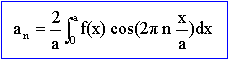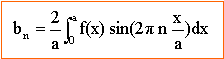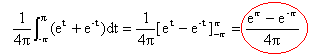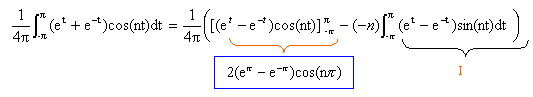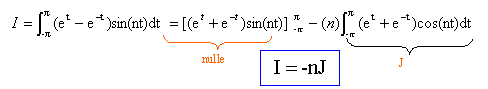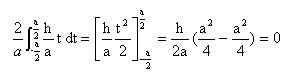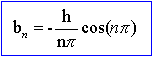|
fonction 1/4 ( et + e-t) fonction en dents de scies En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||
| .
. |
|||
|
|||
|
où a0, an, bn sont des nombres réels appelés coefficients de Fourier réels de f(x). ces coefficients s'obtiennent de la manière suivante :
|
|||
 sur
[-p
; p] sur
[-p
; p]
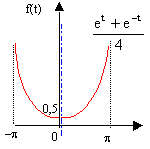
la fonction est symétrique par rapport à l'axe vertical ; f(x) est paire donc bn = 0 calcul de a0 : calcul de an :
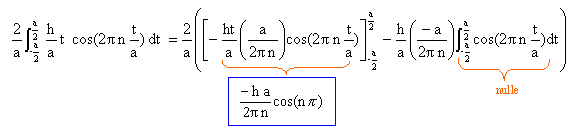
intégration par partie en posant u' = et+e-t ; primitive u = et-e-t ; v = cos(nt) ; dériver v' = -n sin(nt) . calcul de I :
intégration par partie en posant u' = et-e-t ; primitive u = et+e-t ; v = sin(nt) ; dériver v' = n cos(nt) . J est le résultat du premier calcul d'où : J = 2(ep -e-p) cos(np) -n² J par suite J = 2(ep -e-p) cos(np) / (1+n²) et en multipliant J par 1/ (4p) on trouve an. an = (ep -e-p) cos(np) / ((1+n²)2p). a1 = -(ep -e-p) / (4p) ; a2 = (ep -e-p) / (10p) ; a3 = -(ep -e-p) / (20p) ; f(t) = (ep -e-p) / (4p) [ 0,5- cos( t) + 1 / 2,5 cos(2t) - 1 / 5 cos(3t) + ......
|
|||
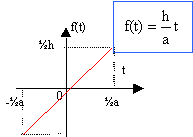 sur [ -½a ; ½a]
sur [ -½a ; ½a]
la fonction est symétrique par rapport à lorigine ; f(t) = - f(-t) est impaire donc an = 0 calcul de a0 : calcul de bn :
intégration par partie en posant u = ht /a ; dériver u' = h/ a ; v' = cos(2pnt / a) ; primitive v = a / 2pn (cos(2pnt / a) . d'où : quelques valeurs : b1 = h/p ; b2 = -h/(2p) ; b3 = h/(3p) |