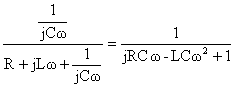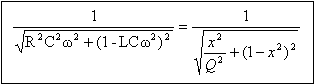Aurélie oct 2001
filtre passe bas d'ordre 2

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

On considère un quadripôle alimenté par une tension alternative sinusoïdale dont on peut faire varier la fréauence.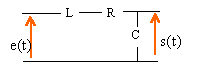

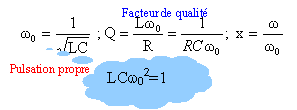
  1. Déterminer la fonction de transfert H(jw).
  2. Exprimer du gain et de la phase en fonction de x et Q.
  3. Construire le diagramme de Bode dans le cas où Q est inférieur ou égal à 0,7
  4. Quel est le rôle du filtre ?

corrigé

toutes les grandeurs soulignées sont des nombres complexes.

A ces grandeurs on peut appliquer les lois du courant continu

Le pont diviseur de tension conduit à :

H(jw) = s / e

expression du gain G(w): norme de la fonction de transfert

remarquons que : w= x w0 ; LCw² = LCw0² x² = x²; RCw= RCw0 x = x/ Q

phase j(w) : argument de la fonction de transfert

tan  j = - RCw / (1-LCw²) = - x / [Q(1-x²)]

j = -tan-1 ( x / [Q(1-x²)] ) si 1-x² >0

j = p +tan-1 ( x / [Q(1-x²)] ) si 1-x² <0

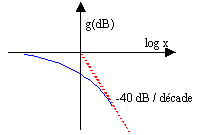
diagramme de Bode en gain :

il s'agit de la représentation graphique de la fonction :

g= -10 log [ x² /Q² + (1-x²)²], g exprimé en décibel (dB)

recherche des asymptotes :

lorsque x tend vers 0+, g tend vers 0-: l'axe des abscisses est asymptote.

lorsque x tend vers l'infini, g tend vers moins l'infini :

(1-x²)² équivalent à x4 et x²/Q² négligeable devant x4

d'où g équivalent à -40 log x équation de l'asymptote (-40 dB par décade)

 

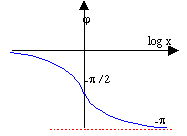
diagramme de Bode de la phase :

j = -tan-1 ( x / [Q(1-x²)] )si 1-x² >0

recherche des asymptotes :

lorsque x tend vers 0+, j tend vers 0-: l'axe des abscisses est asymptote.

j = p + tan-1 ( x / [Q(1-x²)] ) si 1-x² <0

lorsque x tend vers l'infini, j tend vers -p+ : la droite j = -p est asymptote.

valeur particulière j(1) = -½ p .

le filtre est un filtre passe bas d'ordre 2.

retour - menu