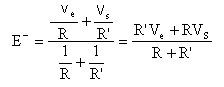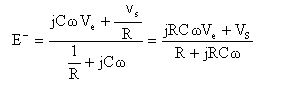|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|
| .
. |
|
|
|
|
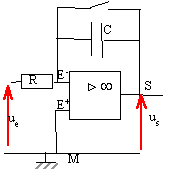
On considère un amplificateur opérationnel idéal. On réalise le montage ci-dessous : 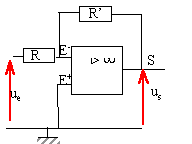
|
|
|
L'A.O fonctionne en régime linéaire( entrée inverseuse E- reliée par l'intermédiaire de R' à la sortie S) Le théorème de Millman permet de déterminer le potentiel E-.
E+ = 0 relié à la masse E+ - E- = e = 0 A.O idéal en conséquence R'Ve+ RVS=0 d'où VS = -R' / R Ve.
second montage : les grandeurs soulignées sont des nombres complexes : à ces nombres on applique les lois du courant continu théorème de Millman :
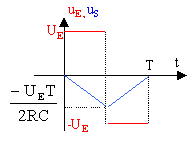
E+ = 0 relié à la masse E+ - E- = e = 0 A.O idéal en conséquence Ve+ jRCwVS=0 VS= -Ve /jRCw . la tension Ve est : d'une part multipliée par -1/(RC) d'où le qualificaif "inverseur" (présence du signe -) d'autre part multipliée par 1/(jw) : cela correspond à une intégration. sur l'intervalle [0 ; ½ T] : ue = UE. us = sur l'intervalle [ ½ T; T] : ue = -UE. us = On détermine la constante en écrivant que la tension uC aux bornes du condensateur est continue. à t= ½ T : uC =-UE T/ (2RC) = UE T/ (2RC) +Cte Cte = -UE T/ (RC) uS = UE (t-T)/ (RC).
On permutte R etC : théorème de Millman :
E+ = 0 relié à la masse E+ - E- = e = 0 A.O idéal en conséquence VS+ jRCwVe=0 VS= -Ve jRCw . la tension Ve est : d'une part multipliée par -RC d'où le qualificaif "inverseur" (présence du signe -) d'autre part multipliée par (jw) : cela correspond à une dérivation. Il apparaît un phénomène de dérive en tension provoquant la saturation de l'A.O. L'intégration donne une fonction affine du temps avec un facteur mutiplicateur : la tension de saturation sera rapidement atteinte. On remédie à ce problème en montant en dérivation sur le condensateur une résistance élevée telle que R >> 1/ Cw.
retour - menu |