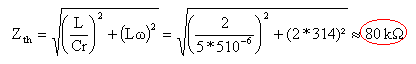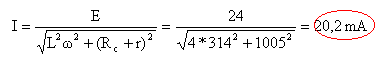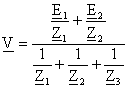Aurélie oct 2001
Norton ; Thévenin ; Milllman

exercice n° 1

exercice n° 2

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

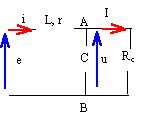
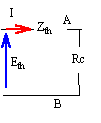
Une source sinusoïdale e est placée en série avec une bobine inductive (inductance L et résistance r) et un condensateur ( capacité C). E eff =24V; f=50 Hz ; L=2 H ; r = 5 W ; Rc = 1 kW.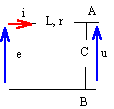

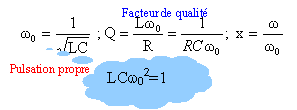
  1. Calculer la valeur de C pour qu'il y ait résonance.
  2. Déterminer Eth et Zth vu des points A et B du modèle équivalent de Thévenin.
  3. On branche une résistance Rc entre A et B.

    - Calculer l'intensité I dans la charge Rc.
    - Quel est le déphasage entre I et e ?

 

corrigé

à la résonance LCw0² =1

w0 = 2p f = 2*3,14*50= 314 rad/s.

L=2 H ; C= 1 / (2*314²) = 5,07 m F.

les grandeurs soulignées sont des nombres complexes : à ces nombres on applique les lois du courant continu

impédance de Thévenin : supprimer la source de tension

les deux dipoles sont en dérivation:

1 / Zth = 1/ (r + jLw) + j Cw = [1 + j Cw(r + jLw)] / (r + jLw)

1 / Zth =[ 1+jCrw-LCw²]/ (r + jLw)

à la résonance 1=LCw² d'où Zth =(r + jLw) / jCrw = L / (Cr) -j /(Cw) = L / (Cr) -j Lw.

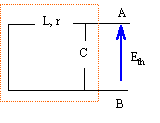
tension de Thévenin : A et B en court circuit

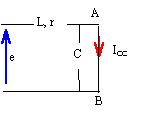
le condensateur est en court circuit

Icc = e / (r+jLw)

puis Eth = Icc Zth = e / (r+jlw) (r + jLw) / jCrw = e / (jCrw) .

charge Rc : circuit équivalent de Thévenin

Eth =I * ( Zth +Rc)

e / (jCrw)= I * [L / (Cr) -j Lw+Rc)

multiplier les deux membres par (jCrw) :

e = I *[jLw+rLCw²+Rc] = I *[jLw+r+Rc]

I = e / [jLw+r+Rc] =e [ -jLw+r+Rc] / [L²w²+(r+Rc)²]

arg I = arg e -arg Z avec arg e=0 (pris comme origine)

arg I = - tan-1(Lw / (r+Rc) = - tan-1( 2*314 / 1005) = -0,56 rad (ou -32°)

l'intensité I dans la charge est en retard sur la tension

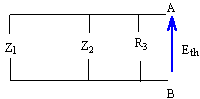
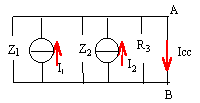
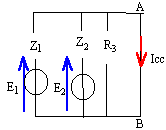
Le montage suivant comporte deux générateurs de fréquence f. E1 = 220 V ; E2 = 110 j volts ; Z1 = 1000j W ;

Z2 = -500j W ; Z3 = R3 =1000 W ;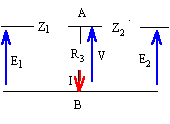

  1. En appliquant le théorème de Millmann déterminer V et I .
  2. En appliquant le théorème de Norton déterminer V et I .
  3. En appliquant le théorème de Thévenin déterminer V et I .
  4. En appliquant le principe de superposition déterminer V et I .
 

corrigé
Millmann :

entre les points A et B trois branches en parallèle.

expression du numérateur : -0,22j -0,22 = -0,22 (1+j)

expression du dénominateur : 10-3 ( -j +2j+1) = 10-3 ( j+1)

V = -220 (1+j) / ( j+1) = -220.

I = V / Z3 = -220/ 1000 = -0,22 A.

Norton ou Thévenin :

on supprime les sources :

1/ Z = 1/ Z1 + / Z2+ 1/ Z3=10-3 ( j+1)

Zth = ZN = Z = 1000 / (j+1) =500(1-j).

calcul du courant de court circuit Icc :
Norton
Thévenin
R3 est en court circuit

Icc = I1 + I2 = E1 / Z1 + E2 / Z2 = -0,22 (1+j)

f e m de Thevenin : Icc * Zth = -0,22 (1+j) *500(1-j) =-220.

I = -220 / 1000 = -0,22 A.

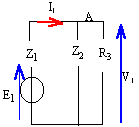
principe de superposition : la source n°1 est seule, on calcule V1 :

 

impédance totale : R3Z2/ (Z2+R3) + Z1 = 200+600 j

V1 = E1 - Z1I1 avec I1 = 220 / ( 200+600 j)

calcul de Z1I1 = 2200j / (2+6j)

V1 = -110 ( 1+j).

la source n°2 est seule, on calcule V2 :

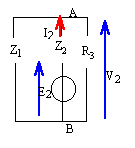
impédance totale : R3Z1/ (Z1+R3) + Z2 = 500

V2 = E2 - Z2I2 avec I2 = 110j / 500 = 0,22 j

calcul de Z2I2 = -500j ( 0,22 j)= 110

V2 = 110 ( j-1).

faire la somme V= V1 + V2 = -220.

I =V/ R3 = -0,22 A.

retour - menu