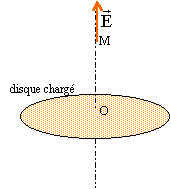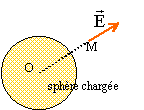|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||||||||||||||||
| .
. |
||||||||||||||||||||
|
||||||||||||||||||||
|
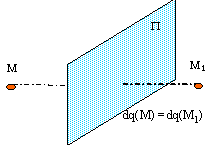
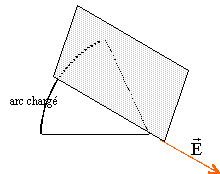
une distribution de charges possède : un plan de symétrie P si pour tout élément symétrique on a des charges identiques. un plan d'antisymétrie P' si pour tout élément symétrique on a des charges opposées.
Une
distribution est invariante
par rotation
si elle reste inchangée par rotation autour d'un axe
: le champ ne dépend pas de l'angle
q.
perpendiculaire
à un plan
d'antisymétrie
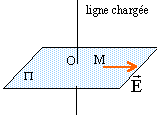
tout plan contenant le fil est plan de
symétrie invariant par translation le long du fil et
invariant par translation le long du fil : donc le champ
dépend de la distance
OM tout plan contenant D
est plan de symétrie le plan du disque est plan de
symétrie. invariant par rotation autour de l'axe
D : donc le champ
dépend de la distance
OM tout plan passant par le centre est plan de
symétrie : champ
radial invariant par rotation autour de tout axe
passant par le centre O : donc le champ
dépend de la distance
OM
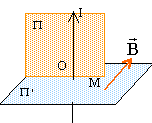
champ magnétique : le champ magnétique est contenu dans un plan d'antisymétrie, perpendiculaire
à un plan de symétrie de la distribution de
courant
tout plan contenant le fil est plan de
symétrie invariant par translation le long de l'axe et
invariant par translation le long de laxe : donc le champ
dépend de la distance
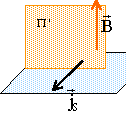
OM tout plan perpendiculaire à jS
est plan d'antisymétrie le plan lui même est plan de
symétrie invariant par toute translation suivant
jS et pour toute translation
perpendiculaire à
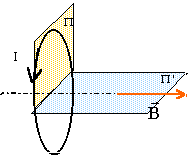
jS. le plan de la spire est plan de
symétrie tout plan contenant l'axe de la spire est plan
d'antisymétrie système invariant par rotation autour de
l'axe. invariance par rotation autour de l'axe invariance par translation |