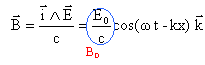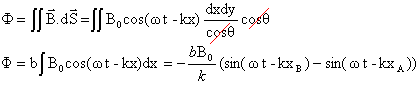Aurélie oct 2001
le phénomène d'induction électromagnétique

Agrég. chimie 91 exercice suivant (déplacement du circuit dans un champ constant )

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

variation temporelle du champ magnétique

On dispose d'une source émettant une onde plane électromagnétique, se propageant dans le sens de l'axe x'x. Une telle onde analogue au rayon lumineux d'un faisceau cylindrique est caractérisée à chaque instant t et en tout point d'abscisse x par :

- un champ électrique noté E.(k = w /c)

- un champ magnétique noté B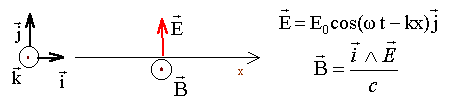

Un cadre conducteur ABCD est placé sur le trajet de l'onde. Le milieu de AB est à l'abscisse x0. Ces dimensions sont AB= a et BC = b; BC est parallèle à y'y.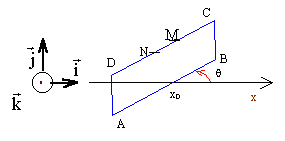

  1.  Montrer que le cadre est parcouru par un courant, dû à l'onde électromagnétique
  2. Déterminer ce courant, si on admet que le cadre posséde une résistance électrique R
flux du champ magnétique variable à travers le cadre fixe ( cas de Neumann)

exprimons le champ magnétique :

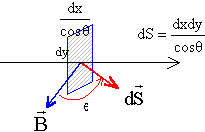
expression de la surface :

expression du flux du champ à travers la surface :

avec xA= x0-½a cosq ; et xB= x0+½a cosq ;

sin p - sin q = 2cos[½(p+q)]sin[½(p-q)]

½(p+q) = wt-½k(xA+xB) =wt-kx0

½(p-q) =½k(xA-xB)= ½kacosq

F = 2bB0 /k cos(wt-kx0) sin (½kacosq)

ce flux dépend du temps ; il existe donc une fem d'induction qui engendre un courant induit dans le cadre.

fem induite e = -dF/dt = 2bB0 w /k sin(wt-kx0) sin (½kacosq)

courant induit : i = e / R

i = 2bB0 w /(kR) sin(wt-kx0) sin (½kacosq) avec B0 = E0 /c et k = w /c

i = 2bE0 /R sin(wt-kx0) sin (½kacosq)

 

retour - menu