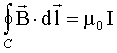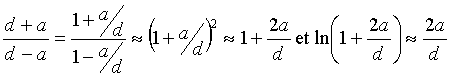Aurélie sept 2001
les courants sources de champs magnétiques

Capes interne 94

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

bobinage torique à section carrée.

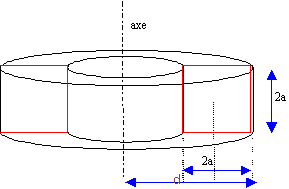
On considère un bobinage de N spires réguliérement réparties sur un tore à section carrée, sans noyau de fer, dont les caractéristiques sont les suivantes : N=200 ; coté du carré 2a=5 cm; distance du centre de l'un des carrés à l'axe du tore d=6 cm.

 

  1. En utilisant les propriétés des symétries justifier que le champ magnétique crée par le bobinage parcouru par un courant continu d'intensité I est orthoradial.
    - Par application du théorème d'Ampère, en déduire l'expression du champ magnétique B(r) à l'intérieur du solénoïde à la distance r de l'axe du tore en fonction de l'intensité du courant I, du nombre de spires N et de la distance r à l'axe.
    - en utilisant le même type de raisonnement montrer que le champ magnétique est nul à l'extérieur du tore.
  2. En déduire l'expression théorique de l'inductance propre L de ce bobinage torique. Dans le cas particulier où a est petit devant d, vérifier que l'on obtient pour L la même formule que celle obtenue dans le cas du solénoïde en posant l=2pd. A.N : Calculer l'intensité I.
La distribution des courants est invariante par rotation d'angle q autour de l'axe du solénoïde : le champ ne dépend donc pas de q.

Tout plan passant par l'axe du tore est plan de symétrie pour les courants : le champ magnétique est donc orthoradial.

les lignes de champ sont des cercles d'axe Oz, Oz étant l'axe du tore.

th. d'Ampère :

On prend une ligne de champ comme contour C. L'intensité enlacée par cette ligne est N I si le point M est à l'intérieur du tore et l'intensité enlacée est nulle si M est extérieur au tore.

Bint 2pr = m0NI et Bext =0

Bint = m0NI / (2pr)

inductance :

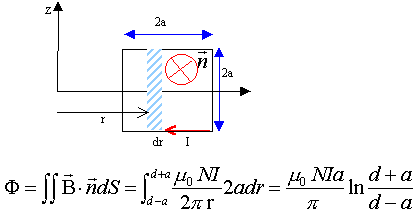
l'inductance L est calculée à partir de l'expression du flux : F=L I.

flux à travers une spire :

flux à travers l'ensemble des spires : multiplier l'expression précédente par N

d'où L = m0N²/p a ln ( (d+a) / (d-a)

a.n : L= 4 p 10-7 *200² / p *0,025 ln (8,5 / 3,5) = 0,355 mH.

si a<<d

alors L voisin de : m0N²/p a * 2a / d

L voisin de : m0N² 4a² /(2pd) soit m0N² S / l

on retrouve la même expression que pour le solénoïde long.

retour - menu