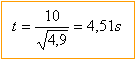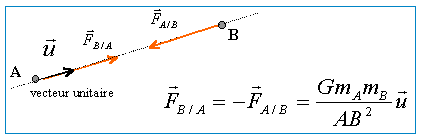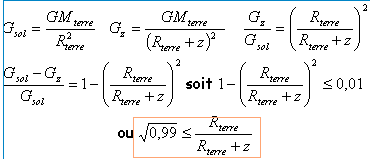|
|
devoirs en
terminale S
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
1
Aristote et Galilée
|
- Aristote (-300 avant JC) affirmait qu'"une masse d'or, de
plomb ou de tout autre corps pesant, tombe d'autant plus vite qu'elle
est grosse"...
- Galilée ( XVII ème siècle) mène une série d'expériences du
haut de la tour de Pise, en Italie. Le savant se munit d'objets divers
et variés : une plume, une pomme, une boule de fer de 100 livres et une
boule de fer de 1 livre...
L'expérience consiste à envoyer par-dessus bord les objets
et observer leur ordre d'arrivée. À l'issue de ce petit jeu, Galilée
affirme que les deux boules arrivent ensemble.
Un an après la mort de Galilée, son élève Evangelista
Toricelli étudie la chute dans le vide d'une plume et d'une pomme. Dans
une enceinte où l'air a été pompé, plume et pomme chutent à la même
vitesse exactement.
- Deux boules de fer de masse respective m = 100 livres et m'
= 1 livre sont lâchées sans vitesse initiale du haut de la tour de
Pise. On considère les actions de l'air comme négligeables par rapport
aux autres forces.
On considère que le mot "vite" utilisé par Aristote fait
référence à la durée de la chute d'un corps à partir d'une hauteur
donnée. Parmi les propositions suivantes, laquelle est soutenue par
Aristote ? Par Galilée ? Justifier votre réponse.
a. t = k / m b. t = k'* m c. t = k''.
k, k' et k'' sont des constantes ; t désigne la durée de
la chute ; m désigne la masse du corps.
- En appliquant les lois de la mécanique aux deux boules de
fer citées ci-dessus et évoluant dans le champ de pesanteur terrestre
considéré comme uniforme de valeur g, exprimer la vitesse de leur
centre d'inertie lorsqu'elles arrivent au sol, ainsi que la durée de
leur chute. Ne pas oublier de faire un schéma.
- Conclure en précisant qui, d'Aristote ou de Galilée, a
raison.
corrigé
|
|
Aristote : durée de la chute et masse sont
inversement proportionnelles donc proposition (a).
Galilée : la durée de la chute est indépendante de la
masse donc proposition (c)
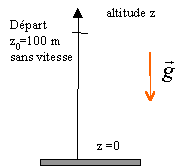
chute libre sans vitesse initiale
altitude : z = -4,9 t²+ 100
en arrivant au sol z=0 d'où la durée de la chute :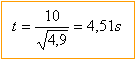
vitesse : dériver z par rapport au temps
v =-9,8 t soit au sol en norme 44,2 m/s.
(le signe moins indique que le vecteur vitesse est dirigé vers
le bas en sens contraire de l'axe z)
La durée et la vitesse sont indépendantes de la masse dans un
mouvement de chute libre ( Galilée a raison)
|
|
2
Newton
et la gravitation
|
Les travaux de Galilée sur la chute des corps, menés du haut
de la Tour de Pise, inspirent, plus de 50 ans après, un Britannique,
Isaac Newton. En 1686, celui-ci annonce une série de lois sur le
mouvement des corps, dont l'une est la "loi de la gravitation
universelle".
- Donner les expressions vectorielles des forces
gravitationnelles s'exerçant entre deux objets ponctuels A et B de
masse respective mA et mB, et situés à une
distance d l'un de l'autre.
- En déduire l'expression du champ de gravitation terrestre
régnant à une altitude z. On notera Gz la valeur de ce champ
de gravitation.
- Si on ne garde que deux chiffres significatifs sur la
valeur de g,valeur du champ de pesanteur, on peut la confondre avec la
valeur Gz du champ de gravitation .
On étudie les variations du champ de gravitation en
fonction de l'altitude : A partir de quelle altitude Gz
varie-t-il de 1 % par rapport à sa valeur au niveau du sol ? En déduire
si les variations de Gz avec l'altitude sont significatives
pour l'expérience de Galilée décrite dans le texte.
- On cherche maintenant à savoir si des objets posés au sol
peuvent modifier de manière significative, du fait de leur masse, la
valeur du champ de gravitation au voisinage de la Terre. Au sol est
maintenant posé un boulet sphérique de rayon 5 cm et de masse m' = 4
kg.
Calculer la valeur maximale du champ gravitationnel que
peut créer le boulet seul, en un point situé à la verticale du boulet.
Conclure.
Données : G = 6,67 10-11 N.m2.kg-2.
Rayon de la terre R = 6 ,371 106 m.
- M (Terre) = 5,99 1021 tonnes. 1 livre = 478 g.
corrigé
|
|
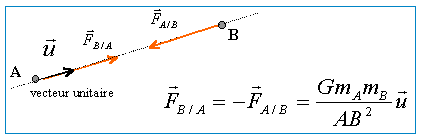
champ de gravitation au sol et à l'altitude z
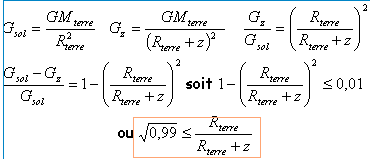
0,9945 (Rterre + z) < 6 ,371 106
Rterre + z <6 ,403 106 soit une
altitude z inférieure à 32 km
(la tour de Pise mesure seulement 100 m)
Champ crée par un boulet de 4 kg à une distance
d supérieure à 5 cm .
6,67 10-11 *4/ d² = 2,67 10-10 / d²
valeur très inférieure à 9,8 ms-2.
A la place du boulet, il faudrait prendre une montagne pour
observser une variation de quelques millièmes.
|
|
 3 3
champ
électrique
|
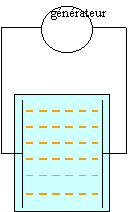
Le but de cet exercice est d'établir les caractéristiques du
champ électrique E régnant entre les deux plaques A et B d'un
condensateur plan et de déterminer la valeur de la différence de
potentiel entre deux points à l'intérieur de ce condensateur. Les deux
plaques du condensateur sont reliées aux bornes d'un générateur de
tension délivrant une tension continue.
A et B sont deux plaques métalliques verticales. Les bases de
A et de B baignent dans de l'huile de ricin. On saupoudre des graines
de gazon entre A et B. Les graines se répartissent à la surface de
l'huile en matérialisant des lignes. Le champ électrique est en tout
point tangent à ces lignes, qui ont l'allure ci contre.
- Quelle(s) caractéristique(s) du vecteur champ électrique
est (sont) mise(s) en évidence dans cette expérience ?
- Les plaques A et B sont toujours verticales, reliées à une
alimentation stabilisée, et on place une petite bille ponctuelle, de
masse m, chargée positivement, suspendue à un fil, entre les armatures.
On constate que la bille est attirée par la plaque B. Peut-on conclure
sur la direction du champ électrique ? Sur son sens ? Si oui, donnez sa
direction et / ou son sens.
corrigé
|
|
|
Les lignes de champ sont parallèles entre elles et
perpendiculaires aux plaques, le champ électrique entre les plaques est
uniforme (vecteur constant en norme et sens).
La bille chargée positivement, placée dans un champ électrique
est soumise à la force électrique 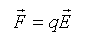
Ces 2 vecteurs colinéaires ont le même sens car q est
positive. Donc le champ électrique est dirigée vers la plaque B.
|
|
 4 4
relation
entre champ et potentiel
|
- Les deux plaques A et B sont verticales, distantes de 12 cm
et immergées dans une cuve horizontale remplie d'une solution aqueuse
de sulfate de cuivre II. Le générateur délivre une tension de 6 V. Un
multimètre muni de pointes-stylet permet de mesurer la différence de
potentiel USB entre différents points S de l'espace entre A
et B et la plaque B. On choisit par convention VB = 0V.
Donnez l'expression de la valeur E du champ électrique au point S.
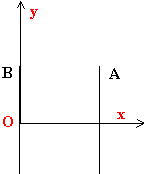
- Soit le repère (Oxy) lié au condensateur, défini ci contre.
Afin de repérer la position du stylet S entre les plaques A et B, on
place sous la cuve un papier millimétré. Les coordonnées du stylet S
sont xS et yS dans le repère (Oxy). On déplace le
stylet de B vers A. Comment la tension USB évolue-t-elle ?
- Pour différentes positions du stylet, on obtient les
valeurs en volts suivantes :
|
yS (cm)
........xS (cm)
|
4
|
2
|
0
|
-2
|
-4
|
|
2
|
1,2
|
1
|
0,8
|
1
|
1,2
|
|
4
|
2,1
|
2
|
2
|
2
|
2,1
|
|
6
|
3
|
2,9
|
3
|
2,9
|
3
|
|
8
|
3,9
|
3,9
|
4
|
3,9
|
3,9
|
|
10
|
4,9
|
4,9
|
4,9
|
4,9
|
4,9
|
-
Quelles sont les observations que l'on peut faire à
la première lecture de ce tableau ?
-
On étudie maintenant la variation du potentiel le
long de la droite y = 0 cm.
Tracer le graphe de la fonction USB = f(xS).
En déduire une relation entre USB et xS. Faire
l'application numérique.
-
En utilisant ce graphique pour xS compris
entre [0 cm ; 12 cm], déterminer la valeur de USB pour x =
12,0 cm et établir pour une position quelconque de S la relation liant USB
, xS et E.
-
On place le stylet au point S de coordonnées ( xS
= 4,0 cm ; yS = 0,0 cm ) dans le repère ci-dessus. La plaque
B reste fixe. On déplace la plaque A jusqu'à ce que xA =
24,0 cm. Quelle sera la valeur de la tension UAB entre les
plaques ? Quelle sera la valeur E du champ électrique entre les plaques
? Quelle sera la tension USB mesurée ?
corrigé
|
|
|
E(Vm-1) = UAB (V) / AB (mètre)
E = 6/0,12 = 50 V m-1.
USB= 50*SB
Si le point S vient en B , USB=0 V
Si le point S vient en A, USB= 50*0,12 = 6 V
La tension USB croît linéairement en allant de B
vers A.
Pour une valeur de x fixée, USB est
quasiment la même, quelle que soit y, si on excepte la ligne où x vaut
2cm.
Pour une valeur de y donnée et pour x croissant la tension USB
augmente.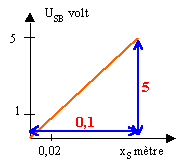
coefficient directeur de la droite 50 V m-1 soit
la valeur du champ E
USB = E xS. soit 6 V pour xS=0,12
m
d' = 2 d
UAB est imposé par le générateur, donc non modifié;
E' = UAB / d' = UAB / (2d )= E / 2
USB = E' x or E' est divisé par 2 , donc USB
est divisée par 2.
|
|
|
|
|
|
|
 3
3
 4
4