Aurélie 06/03

chute d'une balle de ping-pong ; dipôle RLC Amérique 03

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

.

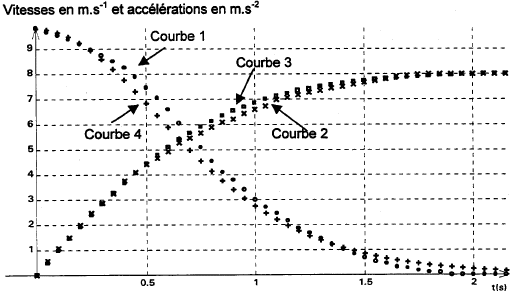
Adrien, Amélie et Benoit étudie la chute d'une balle de ping-pong dans l'air.

masse de la balle : m=2,3 g ; rayon r = 1,9 cm ; g=9,8 m/s² ; masse volumique de l'air : r=1,3 kg m-3 ; volume de la sphère V= 4/3 pr3.

l'objectif est de modéliser le mouvement de chute par une m"thode numérique en faisant l'hypothèse que les frottements dépendent de la vitesse. La première étape consiste à faire le bilan des forces s'exerçant sur la balle. Au bout de quelques minutes ils confrontent leur résultats :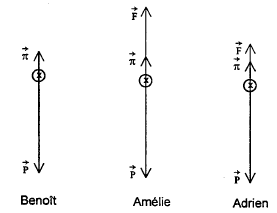

Leur surprise est grande : ils appellent le professeur :

le prof : chacun d'entre vous a à la fois tord et raison, car chaque schéma correspond à une situation particulière. Réfléchissez Adrien : je pense qu'il y a trois forces, le poids P, la poussée d'Archimède P et une force de frottement F.

Amélie : l'un des schémas correspond à l'instant initial, juste quand la balle est lachée ; un autre représente la balle à un temps t quelconque et le 3ème la situation au bout d'un temps très long.

Benoit : ne peut-on pas négliger la poussée devant le poids ?

Amélie : bonne idée, fait le calcul.

Benoit trouve que la poussée est 62 fois plus petite que le poids.

Adrien : On va appliquer la seconde loi de Newton au centre d'inertie du système. Il obtient l'équation (1) : m dv/dt = mg-F

Amélie : on ne connaît pas F.

le prof : plusieurs modèles sont envisageables. Je vous propose de faire l'hypothèse que la valeur de la foce de frottement F est proportionnelle au carré de la vitesse: F=kv². Vous pouvez déterminer k à partir du document ci-dessous :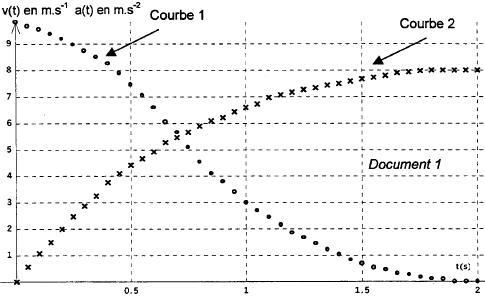

Amélie : l'une des courbes représente l'accélération.

Benoit : on sait qu'à t=0 la vitesse est nulle.

Adrien : on voit que la vitesse tend vers une limite vlim .Adrien se livre à quelques calculs et obtient l'équation (2) : dv/dt = 9,8-0,15 v².

Le professeur propose de résoudre l'équation (2) par la méthode d'Euler à l'aide d'un tableur.

Benoit : il faut connaître les conditions initiales à t=0 , v0 =0 donc (dv/dt)t=0 = 0.

Amélie : le pas d'itération Dt doit être petit.

Benoit : on peut essayer D t=0,05 s.

Amélie : voyons si je peux calculer les premières valeurs. On part de a0 = 9,8 m/s² et v0 = 0. On admet que dv/dt est proche de D v/Dt donc D v = (9,8-0,15v²) Dt soit D v = 0,49 m/s au départ.

Benoit : c'est bien cela; on dit que pendant lae petit intervalle de temps D t, la valeur de la dérivée de la vitesse est constante. On peut en déduire D v et la nouvelle vitesse v.

Amélie : entre t=0 ett =0,05 s, la vitesse est passée de v0=0 à v1= 0,49 m/s.

Benoit : et maintenant on calcule la nouvelle valeur de l'accélération. Je trouve ( dv/dt)t1 = 9,76 m/s² et ainsi de suite par itérations successives.

Questions :

  1. Faire correspondre chaque schéma à une proposition d'Amélie. Justifier.
  2. Calculer le rapport des forces entre le poids et la poussée. Conclure.
  3. Retrouver l'équation (1). Indiquer l'axe de projection utilisé.
  4. Identifier sur le document 1 les deux courbes représentées. Justifier.
  5. Déterminer à partir du document 1 la vitesse limite de la balle. En déduire la valeur expérimentale de k. Retrouver l'équation (2).
  6. Dans le cas d'une sphère de rayon r se déplaçant dans un fluide de masse volumique r, la valeur de k est :
    kt = 0,22r p r2. Calculer la valeur théorique kt. Comparer k et kt et conclure.
  7. Evaluer le temps caractéristique de l'évolution du système. Le choix du pas d'itération vous semble-t-il satisfaisant ? Justifier.
    - Compléter le tableau : justifier.
    temps
    vitesse
    accélération
    t(s)
    v (m/s)
    dv/dt (m/s²)
    0
    0
    9,8
    0,05
    0,49
    0,1
    9,656
    0,15
    1,461
    0,2
    1,935
    9,238
    0,25
    2,397
    8,938
  8. Comparer les valeurs expérimentales ( courbes 1 et 2) et les valeurs calculées avec la méthode d'Euler ( courbes 3 et 4) qui sont rassemblées dans le graphe ci-dessous.

    - Avant de conclure sur la validité du modèle utilisé pour la force de frottement que faut-il modifier dans le calcul numérique ?
    - Quel autre modèle pourrait-on proposer pour la force de frottement ? Expliquer brièvement ce qui serait modifié dans l'équation (2) qui sert de base à la méthode d'Euler.

.
.

corrigé
schéma Benoit : ( poids et poussée ) : F est nulle car la vitesse est nulle au départ.

schéma Adrien : à une date t pas trop grande

schéma Amélie : situation à une date t assez grande ( la force F est d'autant plus grande que la vitesse est grande et la vitesse est une fonction croissante du temps tant que la vitesse limite n'est pas atteinte.

poids : = mg = 2,3 10-3 *9,8 = 2,25 10-2 N

poussée : volume sphère * masse volumique de l'air fois 9,8

poussée = 4*3,14/3*(1,9 10-2)3 *1,3*9,8 = 3,65 10-4 N

poids / poussée = 225/3,65 = 61,6.

suivant un axe vertical orienté vers le bas, la seconde loi de Newton s'écrit : mg-F=mdv/dt

la courbe 2 correspond à la vitesse: valeur nulle au départ, fonction croissante du temps qui tend vers une valeur limite

vlim = 8 m/s.

la courbe 1 correspond à l'accélération : valeur initiale 9,8 m/s², fonction décroissante du temps, l'accélération tend vers zéro lorsque la vitesse limite est atteinte.

Lorsque la vitesse limite est atteinte, le mouvement est rectiligne uniforme : le poids et la force de frottement sont opposées et ont la même valeur :

mg = kv²lim soit k = mg / v²lim = 2,25 10-2 / 8² = 3,51 10-4.

mg-F=mdv/dt avec F= kv²

mg - kv² = mdv/dt ; g-k/m v² = dv/dt (2) avec k/m = 3,51 10-4 / 2,3 10-3 = 0,35 / 2,3 = 0,15.

kt = 0,22r p r2 = 0,22*1,3*3,14*(1,9 10-2)2 = 3,24 10-4.

écart avec la valeur expérimentale 10%: assez bon accord entre théorie et expérience.

La vitesse limite est atteinte au bout de 2 s. Un bon pas d'itération doit être proche de 2/100 = 0,02 s.

La valeur choisie 0,05 s est un peu trop grande et la vitesse limite sera atteinte trop vite..
temps
vitesse
accélération
t(s)
v (m/s)
dv/dt (m/s²)
0
0
9,8
0,05
0,49
9,76
0,1
0,978
9,656
0,15
1,461
9,48
0,2
1,935
9,238
0,25
2,397
8,938
Dv2 = (9,8-0,15 *0,49²) *0,05 = 0,488 m/s.

v2 =v1+Dv2 = 0,49 + 0,488 =0,978 m/s ; a1=Dv2 / D t = 0,488 / 0,05 = 9,76 m/s².

Dv4 =1,935 -1,461 = 0,474 m/s ; a3 = Dv2 / D t = 0,474 / 0,05 = 9,48 m/s².

Les courbes 1 et 2 (valeurs expérimentales) et les courbes 3 et 4 ( valeurs calculées avec la méthode d'Euler )ne coîncident pas tout à fait. La valeur choisie pour le pas d'itération 0,05 s est un peu trop grande et la vitesse limite sera atteinte trop vite.

Prendre un pas de 0,02 s avant de conclure sur la validité du modèle.

Un autre modèle pour la force de frottement : F est proportionnelle à la vitesse, F=k1v.

(2) s'écrirait alors : dv/dt = 9,8-k1/m v

dipôle RLC (4 points)

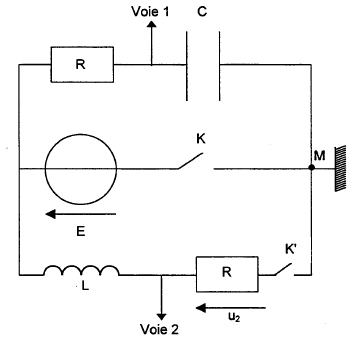
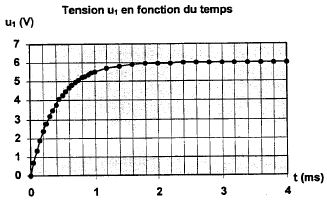
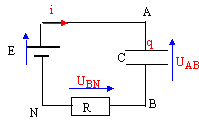
E=6 V ; la résistance de la bobine est négligeable. On visualise sur la voie 1 la tension u1 aux bornes du condensateur en fonction du temps.

expérience 1 : on ferme K ( en maintenant K' ouvert). Le dipôle RC est alors soumis à un échelon de tension de valeur E.

  1. Quel est le nom du phénomène observé sur la voie 1 à la fermeture de K.
  2. Reproduire sur la copie la partie du circuit concerné et indiquer sur ce schéma, juste après la fermeture de K, le sens du courant, le signe des charges de chacune des armatures du condensateur. Indiquer la flèche tension u1 aux bornes du condensateur.
  3. Sur la voie 1 on obtient la courbe ci-dessous :

    Déterminer graphiquement la constante de temps t du dipôle (RC) en expliquant la méthode utilisée. Sachant que R= 20 W en déduire la valeur de la capacité C.

  4. L'étude théorique du dipôle RC conduit à l'équation différentielle t du1/dt + u1 = E. Retrouver cette équation différentielle en appliquant la loi d'additivité des tensions.
    - Compte tenu des conditions initiales, la solution de cette équation s'écrit u1 = E[1-exp(-t/t)]. Calculer u1 pour t=5t. Conclure.

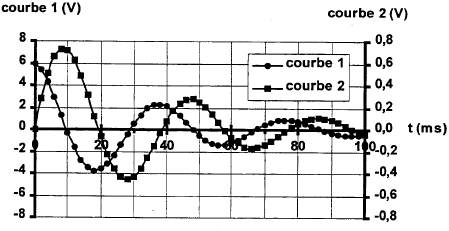
Expérience 2 : une fois la première expérience réalisée on ouvre K et on ferme K'. Le circuit est alors le siège d'oscillations électriques. On visualise sur la voie 1 la tension u1 aux bornes du concensateur et sur la voie 2, la tension u2 aux bornes du conducteur ohmique R. L'acquisition est synchronisée avec la fermeture de l'interrupteur.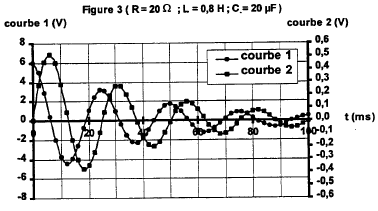

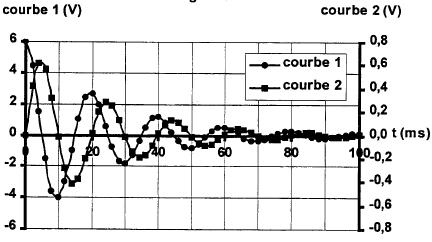
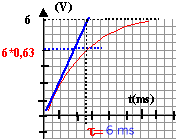
  1. Attribuer à chaque courbe la tension correspondante. Justifier.
  2. mesurer la pseudo-période T des oscillations. Calculer la période propre T0. Conclure.
  3. Influence des paramètres : on réalise la seconde expérience en modifiant un seul des paramètres L ou C. Deux cas sont proposés. Dans l'un on a diminué la valeur de L, dans l'autre on a augmenté la valeur de C. Attribuer à chaque cas la figure qui lui correspond. Justifier.

corrigé
charge d'un condensateur.

q positive et u1 = uAB. B porte la charge -q.

à t = t , u1 vaut 0,63 E = 3,8 V

tracer une horizontale passant par 3,8 V; l'intersection avec la courbe donne t = 0,4 ms= 4 10-4 s

tracer la tangente à t=0 : celle ci coupe l'asymptote oblique à t = t

uBN+uAB=E ; Ri + u1 = E avec i= dq/dt = Cdu1/dt

RCdu1/dt+ u1 = E avec t = RC

t = 4 10-4 = 20 C d'où C = 2 10-5 F.

u1 ( t=5t) = 6 (1 - exp(-5))= 5,96 V

le condensateur est pratiquement chargé à t = 5t.

La courbe 1 correspond à la tension aux bornes du condensateur : à t=0, fermeture de K' la tension aux bornes du condensateur vaut 6 V.

La courbe 2 correspond à la tension aux bornes du conducteur ohmique u2 = Ri: à t = 0 l'intensité du courant est nulle.

T( lecture graphe) voisine de : 25 ms = 2,5 10-2 s.

T0 = 2p(LC)½ = 6,28(0,8*2 10-5)½ = 2,51 10-2 s.

T0 et T sont proches, les oscillations sont peu amorties.

En diminuant la valeur de L, C étant constant, la période T diminue ( figure 5)

et en augmentant la valeur de C, L étant constant, T augmente ( courbe 4)

à suivre ...
retour - menu
à bientôt ...