|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
En aout 2009, l'ESA envera simultanément deux sondes vers la planète Mercure. Les deux sondes seront mises en orbite autour de Mercure. L'une l'orbiteur "magnétosphérique" chargée d'étudier le champ magnétique sera placée en orbite elliptique. L'autre l'"orbiteur planétaire" , chargée de prendre des photos de la surface sera placée sur une trajectoire circulaire de rayon r =3,5 103 km. G= 6,67 10-11 S.I ; masse de mercure M= 3,3 1023 kg.
référentiel : Mercure origine du repère : le centre de mercure les trois axes pointent vers des étoiles lointaines fixes. force de gravitation : F : force en newton ; G constante de gravitation ; M et m : masse en kg ; r distance du centre de Mercure au satellite exprimée en mètre. l'orbiteur exerce sur Mercure une force opposée à la force exercée par Mercure sur l'orbiteur ( 3ème loi de Newton). ces deux forces ont la même norme.
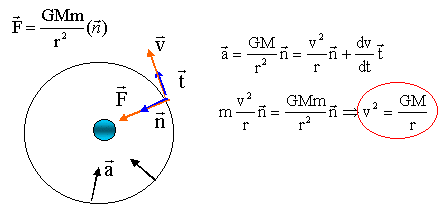
L'accélération est centripète. L'orbiteur est soumis à la seule force de gravitation centripète, perpendiculaire à la vitesse : en conséquence cette force ne travaille pas et ne modifie pas l'énergie cinétique de l'orbiteur. La valeur de la vitesse de l'orbiteur est constante : le mouvement est uniforme. v² = GM/ r = 6,67 10-11 * 3,3 1023 / 3,5 106 = 6,3 106 v= 2,5 103 m/s. 2p est sans dimension (1) r / (GM) : r longueur ; M masse en kg ; G : L3M-1T-2 soit L L-3M1T2 M-1 ; soit L-2T2 (2) GM/r3 : r longueur ; M masse en kg ; G : L3M-1T-2 soit L3M-1T-2 M L-3 ; soit T-2 (3) r3 / (GM) : r longueur ; M masse en kg ; G : L3M-1T-2 soit L3 L-3M1T2 M-1; soit T2 expression correcte. T = 2*3,14 ((3,5 106)3 / (6,67 10-11 * 3,3 1023))½=8,76 103 s = 2 h 26min. La planète tourne autour d'un axe passant par les pôles et l'orbiteur a une orbite polaire : ce dernier peut survoler et photographier toute la surface de Mercure au cours de plusieurs révolutions.
|
|||||
|