|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
Deux enfants Amélie et Benoît sont sur un balcon. Ils jouent avec des palets de hockey identiques, et, au cours de leurs différentes parties, ils s’interrogent...... 1. Première partie : Amélie lâche son palet A sans vitesse initiale, et, en même temps, de la même altitude par rapport au sol, Benoît lance son palet B avec une vitesse initiale horizontale v0 . Benoît pense que son palet touchera le sol plus tard que celui d’Amélie. La modélisation est la suivante : - les palets sont assimilés à des points matériels (confondus avec leur centre d’inertie) de masse M, - les actions de l’air sont négligeables par rapport aux autres forces, - les palets sont initialement à une altitude h = 5,0 m par rapport au sol (voir schéma n° 1). 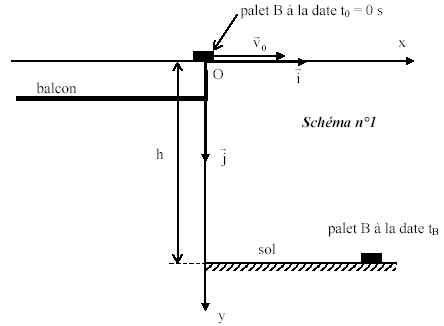 On considérera que le référentiel terrestre est galiléen et on prendra pour accélération de la pesanteur g = 10 m.s-2.
2. Deuxième partie : Amélie et Benoît décident de comparer leur force. Une gouttière lisse et horizontale leur sert de rampe de lancement. L'un après l'autre, chacun d'eux place son palet en K et le pousse jusqu’au point O où le palet quitte la rampe. Le palet A touche le sol à la distance DA = 8,0 m du pied H du balcon , le point H appartenant au plan vertical xOy. Le palet B touche le sol à la distance DB = 4,0 m de H. Amélie affirme à Benoît : « je suis deux fois plus forte que toi. ». On se propose de savoir si elle a raison. 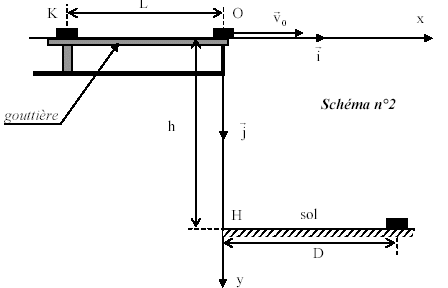 L’étude dynamique du mouvement du centre d’inertie du palet dans la phase de chute conduit à l’expression : où v0 est la valeur de la vitesse en O. On modélise l’action des mains d’Amélie (ou de Benoît) sur un palet par une force horizontale constante F qui s’exerce sur la distance KO = L = 1,0 m. La vitesse en K est nulle (voir schéma n° 2). Les forces de frottement agissant sur un palet sont négligées par rapport aux autres forces.
3. Troisième partie : Amélie se demande quelle vitesse devrait avoir le palet s’il tournait au voisinage de la surface de la Terre. Le mouvement supposé du palet peut être assimilé, dans ce cas, à un mouvement circulaire de centre T, centre de la Terre, et de rayon R = 6,4 ×103 km.
les vecteurs sont écrits en gras. B : chute libre avec vitesse initiale vitesse initiale v0 ( v0 ; 0) ; accélération a=g(0 ; g) ;position initiale : origine du repère la vitesse est une primitive de l'accélération : v(v0 ; gt) le vecteur position est une primitive de la vitesse : OM( xB= v0t ; yB = ½gt²) trajectoire : yB = ½g xB² / v0² ; les palets arrivent en même temps au sol car yA = yB quel que soit t. arrivée au sol :
t²B = 2h / g = 1 soit tB = 1s.
R action du support, perpendiculaire au sol, vers le haut, opposée au poids. F : force musculaire, horizontale à droite. poids et action du support, perpendiculaires à la vitesse ne travaillent pas. Le travail de F est moteur sur le parcours KO=L et vaut F.KO = F L variation d'énergie cinétique au cours du parcours KO : DEc = ½mv0²-0 = FL v0² = 2FL / m ou F = v0² m / (2L) or v0² = D²g / (2h) d'après le texte F= D²gm / (4Lh) = constante * D² la force est
proportionnelle au carré de la distance D : si D double alors la force
quadruple.
Le mouvement circulaire est étudié dans le référentiel géocentrique. Le palet est soumis uniquement à la force de gravitation centripète, perpendiculaire au vecteur vitesse : en conséquence cette force ne travaille pas et ne modifie pas l'énergie cinétique. la norme de la vitesse reste constante et le mouvement est uniforme. accélération centripète : g0= GMterre/ R² = v²/R soit v² = gR = 10 * 6,4 103 = 6,4 104 v = 2,53 102 km/s.
|
|||||
|