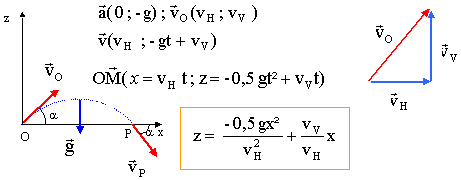Aurélie 09 /02

le jongleur à cheval la Réunion 02

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


On se pose la question suivante : si un jongleur à cheval lance en l'air verticalement une balle, celle-ci retombera-t-elle toujours dans la main du cavalier ?

Soit B le centre d'inertie de la balle. Soit A le point auquel on assimile la main du cavalier. Soit C le centre d'inertie du système {cheval+ cavalier}. Le mouvement de B et C sont étudiés dans le référentiel terrestre supposé galiléen. Le point C se déplace parallèlement à l'axe horizontal. Le vecteur vH du point C est constant.( un vecteur est écrit en gras et en bleu). Après le lancer le mouvement de la main est le même que celui de C. On prend comme origine des dates, l'instant où la balle quitte la main du cavalier. Les points A, B et O sont alors confondus.

  1. Rappeler la définition d'un repère galiléen.
    - Préciser la nature du mouvement du point C.
  2. Avant le lancer, le vecteur vitesse du point B est le même que celui du point A soit vH. On donne vH=5m/s. Le cavalier lance la balle en lui communiquant une vitesse verticale vV de valeur vV = 7 m/s. Représenter les vecteurs vH , vV et leur somme vO au point O.
  3. La trajectoire suivie par B se situe dans le plan( O, i, k). Les forces de frottement sont négligées :
    - Faire le bilan des forces agissant sur la balle après le lancer.
    - Appliquer la deuxième loi de Newton au point B; en déduire les équations horaires xB(t) et zB(t) du mouvement de B.
    - En déduire l'équation de la trajectoire.
  4. Le centre d'inertie du projectile recoupe l'axe (Ox) en un point P. Exprimer littéralement puis calculer :
    - la date tP de l'instant où se produit l'évenement.
    - les coordonnées xP et zP du point P.
  5. Préciser les expressions littérales des équations horaires xA(t) et zA(t) du point A.
    - le jongleur récupérera-t-il la balle et cela quelle que soit la valeur de la vitesse initiale vV ? Justifier.
  6. Donner les expressions de vO et vS ( vitesse de la balle au sommet de sa trajectoire) en fonction de vH et vV.
  7. En appliquant le théorème de l'énergie cinétique à la balle, déterminer :
    - l'expression littérale de la hauteur maximale h atteinte en fonction de g et de vV.
    - l'expression litérale de la vitesse vP de la balle lorsque le jongleur la récupère.
    - comparer les caractéristiques de     vO , vP.

 

.
.

corrigé
dans un référentiel galiléen le centre d'inertie d'un système pseudo-isolé ( somme des vecteurs forces nulles) est soit au repos soit animé d'un mouvement rectiligne uniforme et réciproquement.

Le mouvement de C est rectiligne uniforme.( le vecteur vitesse vH étant constant)

le point P :

zP=0 soit -0,5 gt² +vV tP=0 d'où : tP= 2vV/g

xP= vH tP = 2vHvV/g.

le point A :

la main reste immobile, le point A a le même mouvement rectiligne uniforme que le centre d'inertie du système C.

zA=0 ; xA= vH t

en conséquence xP= xA quel que soit la vitesse initiale vH. Le jongleur récupère la balle tant que le vecteur vH est constant.

au sommet S de la trajectoire, la composante verticale de la vitesse est nulle ( la tangente à l'arc de parabole est horizontale)

vS ( vH ; 0)

théorème de l'énergie cinétique entre l'instant de départ et l'instant de passage au sommet S:

seul le poids travaille : W= -mgh ( signe moins car ça monte)

DEc = Ecfinale en S - Ec initiale = ½m ( v²S-v²O)

v²S= v²H et v²O= v²H + v²V .

DEc = -mgh = ½m (- v²V ) d'où h = v²V /(2g).

au point P, les composantes de la vitesse sont : vP ( vH ; -gtP+vV)

avec tP = 2vV/g.

vP ( vH ; -gtP+vV) soit vP ( vH ; -vV)

voir graphe ci-dessus

à suivre ...
retour - menu
à bientôt ...